Общая характеристика переходных процессов электроприводов, их классификация и методы расчета
Переходным процессом или переходным режимом электропривода называется режим его работы при переходе от одного установившегося состояния к другому, когда изменяется скорость, ток, момент. Причинами возникновения переходных режимов в электроприводах является либо изменение нагрузки, связанное с производственным процессом, либо воздействие на электропривод при управлении им, т.е. пуск, изменение скорости, торможение, реверс и т.п. Переходные режимы могут возникнуть также в результате аварии или других случайных причин, например, при изменении величины напряжения или частоты сети, несимметрии напряжения по фазам, изменении порядка следования фаз, полном исчезновении напряжения, обрыве проводов и т.п. У некоторых механизмов, таких как кривошипно-шатунные прессы, ножницы, подъемно-качающиеся столы некоторых прокатных станов установившихся режимов вообще нет, а их рабочие режимы представляют собой периодические переходные процессы.
Переходные режимы играют огромную роль в работе электропривода и механизма и часто их характер предопределяет производительность механизма и качество выпускаемой продукции. Поэтому изучение этих режимов имеет большое практическое значение. Анализ этих режимов дает возможность детально выявить поведение электропривода, произвести правильный его выбор и расчет мощности электродвигателя, уменьшить расход энергии при пуске и торможении и т.д. Анализ переходных режимов позволяет также выявить предельно допустимое с т.з.нагрева число включений в час двигателя электропривода, работающего большую часть времени в переходных режимах.
Лишь ограниченное число механизмов допускает возможность проектирования их электропривода без учета характера протекания переходных процессов. К ним относятся некоторые редко пускаемые и длительно работающие механизмы с простейшими пусковыми устройствами, например, вентиляторы, насосы, а также механизмы, в которых производственный процесс настолько груб, что к их электроприводу вообще не предъявляется каких-либо особых требований, кроме обеспечения заданной мощности (бетономешалки, камнедробилки и т.п.).
Характер переходного режима электропривода зависит от свойств рабочей машины, типа электродвигателя, передачи, режима работы двигателя (пуск, торможение, сброс или наброс нагрузки и т.п.). Теоретическое рассмотрение переходных процессов с учетом всех влияющих факторов часто затруднителен, ибо не всегда можно аналитически выразить законы изменения отдельных параметров или же поведение электропривода в переходных режимах описывается системой уравнений высоких порядков. К счастью, далеко не во всех случаях требуется детальный учет всех факторов. Второстепенные факторы, которые при решении каждой конкретной задачи не могут оказать заметного влияния на поведение электропривода, могут не приниматься во внимание.
На протекание переходных процессов значительное влияние оказывает механическая, электромагнитная и тепловая инерция. Механическая инерция, характеризуемая электромеханической постоянной Тм , зависит как от инерционных масс и характера Мс , так и от электромеханических свойств двигателя. Электромагнитная инерция характеризуется электромагнитной постоянной Тэ , зависящей от L и R электрической цепи.Тепловая инерция характеризуется постоянной времени нагрева Тн, зависит от теплоемкости машины и ее теплоотдачи. Поскольку тепловые процессы протекают значительно медленнее электромагнитных и механических, их при анализе переходных процессов электропривода не принимают во внимание.
Следует иметь в виду, что если механическая инерция практически всегда ощутима и сказывается на переходных процессах, то электромагнитная инерция может быть и несущественной и практически не влиять на характер протекания процессов. В связи с этим, когда не требуется очень большой точности, ограничиваются только механической инерции. Переходные процессы в этом случае называются механическими. Если учитывается только электромагнитная инерция ( например в цепях возбуждения) , переходные процессы называются электромагнитными. Переходные процессы, в которых учитывается как механическая, так и электромагнитная инерция, называются электромеханическими.
Переход из одного установившегося режима к другому может совершаться по различным траекториям. При управлении электроприводом нужно стремиться выбирать такие, которые обеспечивают максимальное быстродействие, минимум потерь энергии и динамических нагрузок, максимум полезной работы и оптимальные значения других показателей.
 Наиболее часто требуется обеспечить изменение скорости электропривода за минимальное время при ограничении момента двигателя. Такие переходные процессы называются оптимальными по быстродействию при ограничении момента. Этому условию при Мс=const соответствует равномерно ускоренный характер изменения скорости при М=Мдоп=cconst (см. кривые 1 и 2 на рис.)
Наиболее часто требуется обеспечить изменение скорости электропривода за минимальное время при ограничении момента двигателя. Такие переходные процессы называются оптимальными по быстродействию при ограничении момента. Этому условию при Мс=const соответствует равномерно ускоренный характер изменения скорости при М=Мдоп=cconst (см. кривые 1 и 2 на рис.)
Если Мс=f(w), то скорость w при реверсе в процессе торможения и пуска должна изменяться с различными ускорениями в случае реактивного Мс , как показано на рисунке. Для некоторых производственных механизмов, например, пассажирских лифтов, переходные процессы электропривода должны протекать при строго ограниченном ускорении. Условием минимальной длительности переходного процесса является поддержание постоянства ускорения при различных нагрузках. Такие переходные процессы называются оптимальными по быстродействию при ограничении ускорения e.
В этом случае зависимость w=f(t) должна оставаться неизменной при разных Мс, а момент двигателя  при этих разных Мс будет изменяться.
при этих разных Мс будет изменяться.
 Однако в ряде случаев момент двигателя не реагирует на изменение нагрузки. В этом случае для ограничения e при любых Мс допустимый пусковой момент двигателя необходимо выбрать из условия
Однако в ряде случаев момент двигателя не реагирует на изменение нагрузки. В этом случае для ограничения e при любых Мс допустимый пусковой момент двигателя необходимо выбрать из условия 
Ускорение электропривода при возрастании нагрузки будет уменьшаться и при Мс=Мс макс
примет значение 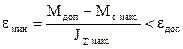 Время пуска по мере возрастания нагрузки, очевидно, будет увеличиваться.
Время пуска по мере возрастания нагрузки, очевидно, будет увеличиваться.
Переходные процессы, в которых требуется обеспечить плавность их протекания путем ограничения производной момента 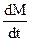 или т.н. рывка
или т.н. рывка  наряду с ограничением момента или ускорения называются оптимальными при ограничении момента или ускорения и рывка.
наряду с ограничением момента или ускорения называются оптимальными при ограничении момента или ускорения и рывка.
Необходимость таких ограничений вызывается различными причинами. Так для двигателей постоянного тока по условиям коммутации необходимо ограничивать 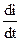 , следовательно,
, следовательно,
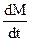 .Для пассажирских лифтов ограничение рывка создает более комфортные условия. Нужно иметь в виду, что ограничение производной
.Для пассажирских лифтов ограничение рывка создает более комфортные условия. Нужно иметь в виду, что ограничение производной 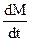 при пуске электропривода влечет за собой снижение быстродействия, т.к. , например, время пуска возрастает при уменьшения
при пуске электропривода влечет за собой снижение быстродействия, т.к. , например, время пуска возрастает при уменьшения 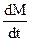 .
.
Переходные процессы в реальных электромеханических системах описываются нелинейными дифференциальными уравнениями и расчет этих процессов возможен с помощью ЭВМ. Но первичными и более наглядными все же остаются аналитические и графоаналитические методы анализа переходных процессов. К ним относятся :
1.Метод последовательных интервалов (численный метод интегрирования исходных уравнений).
2.Метод кусочно-линейной аппроксимации нелинейных характеристик.
3.Метод фазовой плоскости.
4.Метод гармонической линеаризации.
5.Метод линеаризации уравнений в окрестностях точки статического равновесия путем разложения в ряд Тейлора.
Первый и третий методы используются для анализа переходных процессов в существенно нелинейных системах. Метод фазовой плоскости применим для анализа процессов в системах не выше второго порядка, а первый метод – в системах до третьего порядка. Наиболее широко применяются второй и пятый методы. Так, второй метод позволяет аналитически исследовать процессы в электроприводах, дифференциальные уравнения которых не содержат произведений переменных, а нелинейные характеристики удовлетворительно линеаризуются двумя – тремя отрезками прямых. При наличии в уравнениях произведений переменных, линеаризация математического описания производится размножением в ряд Тейлора.
При использование кусочно-линейной аппроксимации и разложении в ряд Тейлора анализ переходных процессов ведется путем решения дифференциальных уравнений классическим либо операторным методом. В дальнейшем используем классический метод.
Уравнения электромеханического переходного процесса электропривода с линейной механической характеристикой при Мс=const и w0=const
В большинстве применяемых в промышленности электроприводов, получающих питание от сети, электромеханические переходные процессы протекают при неизменном напряжении Uя или частоте f1, т.е. при w0=const. Переходные процессы при этих условиях возникают при изменении управляющего воздействия w0 или f1 скачком (пуск,торможение, реверс, отключение от сети) или изменение нагрузки ( скачок нагрузки). Для ограничения тока при пуске или торможении до допустимых значений в цепь якоря или ротора двигателя вводится добавочное сопротивление. При этом электромагнитная постоянная 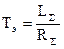 силовой цепи значительно снижается, а электромеханическая постоянная Тм, наоборот, увеличивается, т.к.
силовой цепи значительно снижается, а электромеханическая постоянная Тм, наоборот, увеличивается, т.к.  , (уменьшается жесткость b). Поэтому при работе двигателя на пусковых характеристиках влиянием электромагнитной инерции на течение переходных процессов можно пренебречь, считая Тэ=0.
, (уменьшается жесткость b). Поэтому при работе двигателя на пусковых характеристиках влиянием электромагнитной инерции на течение переходных процессов можно пренебречь, считая Тэ=0.
Необходимость учета Тэ обычно возникает при выходе двигателя для работы на естественной характеристике, когда добавочные сопротивления полностью выведены и влияние электромагнитной инерции может быть существенным.
Получим уравнения переходного процесса для общего случая при Тэ=0 и ненулевых начальных условиях. Электромеханические переходные процессы при жестких механических связях, т.е.  , описываются уравнениями
, описываются уравнениями
 ;
; 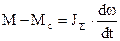
Найдя из второго уравнения М и подставив в первое, получим уравнение, разрешенное относительно w 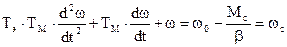
Аналогично можно получить уравнение, разрешенное относительно М

Корни характеристического уравнения этих дифференциальных уравнений при 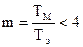
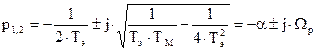
Общее решение этих уравнений при m<4
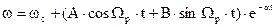
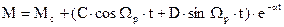
Постоянные интегрирования A, B, C, D находятся из начальных условий.
При t=0 w=wнач ; M=Mнач ; 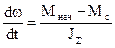
wнач=wc+A ; Mнач=Мс+С 
отсюда  ; С=Мнач-Мс ;
; С=Мнач-Мс ; 

отсюда 
Т.о. законы изменения w и М будут такими:
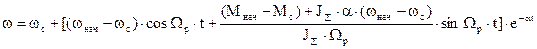
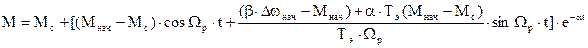
При 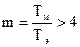 корни р1=-a1 ; р2=-a2 и общее решение дифференциальных уравнений относительно w и М имеет вид
корни р1=-a1 ; р2=-a2 и общее решение дифференциальных уравнений относительно w и М имеет вид
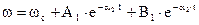

Постоянные интегрирования определяются аналогично предыдущему случаю исходя из начальных условий. Законы изменения w и М будут такими:
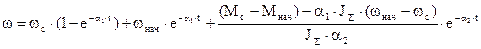
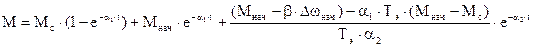
При  , что бывает в редких случаях, р1=р2=a и общее решение дифференциальных уравнений относительно w и М имеет вид
, что бывает в редких случаях, р1=р2=a и общее решение дифференциальных уравнений относительно w и М имеет вид
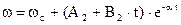

Коэффициенты А2, В2, С2, D2 находятся из начальных условий.
Полученные общие зависимости в частных случаях существенно упрощаются, если до начала переходного процесса режим работы электропривода был установившимся.
Во всех случаях, когда двигатель работает на реостатных характеристиках, Тэ пренебрежительно мала и можно считать ее равной 0. Если электромеханическая связь в системе электропривода является жесткой, уравнения переходного процесса можно получить из соотношений для случая m>4, положив в них 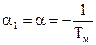 и
и 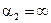
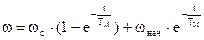
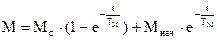
Переходный процесс электропривода с линейной механической характеристикой при одно и многоступенчатом пуске в случае Мс=const; w0=const
При одноступенчатом пуске переходный процесс описывается уравнениями
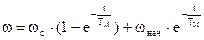 ;
; 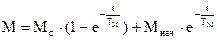
если увеличение скорости происходит не от w=0, а от какого-то начального установившегося
 |
значения, как показано на графиках. Закон изменения ускорения

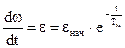 , где
, где 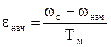
Уменьшение e по мере увеличения скорости объясняется непрерывным уменьшением динамического момента Мдин. Если разгон идет из неподвижного состояния, т.е. когда wнач=0 , то
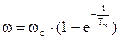

Время разгона на любом участке процесса до какой либо промежуточной скорости wкон

Т.к. wкон=wc , то  . Практически процесс считается закончившимся, когда разность между установившимся и текущим значением w снижается до 2%, т.е.
. Практически процесс считается закончившимся, когда разность между установившимся и текущим значением w снижается до 2%, т.е.
 или
или 
При wнач=0 wкон=0,98wс . поэтому

Обычно принимается t=(3-4)Tм
Величину Тм можно определить проведя касательную в любой точке кривой w(t) или М(t), например, в начале координат, как показано на графиках или используя следующие выражения
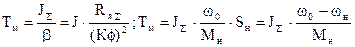
Для расчета переходного процесса при многоступенчатом пуске сначала строится пусковая диаграмма по ранее изложенным правилам задавшись пусковым и переключающим моментами.  Для любой ступени разгона время, в течение которого момент изменяется от М1 до М2 может быть определено по формуле
Для любой ступени разгона время, в течение которого момент изменяется от М1 до М2 может быть определено по формуле 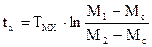
Постоянная времени для любой ступени разгона
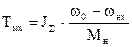
Законы изменения w и М при разгоне на любой ступени определяются согласно ранее приведенным выражениям.
Для примера рассчитаем переходный процесс на первой и второй ступенях. Сначала для первой ступени
1. 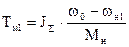 3.
3. 
2.  4.
4. 
Значения wн1 и wс1 находятся из графика, где изображена пусковая диаграмма при М=Мн и М=Мс . Задаваясь временем t от 0 до t1 , рассчитываются законы изменения w и М на первой ступени и строятся кривые w=f(t) и M=f(t).
Далее делается расчет процесса на второй ступени
1. 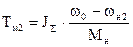 3.
3. 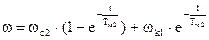
2.  4.
4. 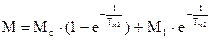
Значения wс2 и wк1 находятся из пусковой диаграммы. Задавясь временем t от 0 до t2, рассчитываются и строятся кривые w=f(t) и M=f(t) для второй ступени и т.д. Время разгона на естественной характеристике до w=wн=wс принимается равным tн=(3-4)Tм, где в Тм вместо wнх подставляется wн.
Переходные процессы электропривода с линейной механической характеристикой при Мс=const, w0=const в тормозных режимах
Рассмотрим сначала реверс, который заключается в торможении противовключением с дальнейшим изменением направления вращения и разгоне в противоположную сторону.
Если реверс осуществляется при активном моменте сопротивления Мс=const, переходный процесс описывается уравнениями, приведенными ранее для двигательного режима, с той разницей, что в выражениях для w и М нужно поставить знак минус перед wс и перед Мнач
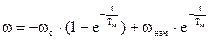

На графике с механическими характеристиками показан переход из двигательного режима в режим противовключения и построены кривые переходного процесса. Двигатель при переводе его  в режим противовключения тормозится по линии ВС. Затем, если его не отключить от сети, будет разгоняться в обратном направлении по линии CD, достигает скорости идеального холостого хода (-w0) и т.к. момент сопротивления активный, переходит в генераторный режим с отдачей энергии в сеть (линия DE). Равновесие наступит в т.Е, где М=Мс и скорость w=-wс .Такой процесс может быть, если в случае подъема тяжелого груза двигатель тормозится противовключением и при w=0 не отключается и не затормаживается механическими тормозами.
в режим противовключения тормозится по линии ВС. Затем, если его не отключить от сети, будет разгоняться в обратном направлении по линии CD, достигает скорости идеального холостого хода (-w0) и т.к. момент сопротивления активный, переходит в генераторный режим с отдачей энергии в сеть (линия DE). Равновесие наступит в т.Е, где М=Мс и скорость w=-wс .Такой процесс может быть, если в случае подъема тяжелого груза двигатель тормозится противовключением и при w=0 не отключается и не затормаживается механическими тормозами.
При реактивном моменте сопротивления процесс разбивается на два этапа. На первом этапе, являющемся тормозным, законы изменения w и М описываются теми же уравнениями что и при активном Мc. Время торможения до w=0 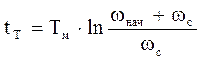 , где - wс- фиктивная скорость, к которой стремиться двигатель.
, где - wс- фиктивная скорость, к которой стремиться двигатель.
 |
На втором этапе происходит разгон в противоположном направлении (после торможения противовключением и остановки). Знак Мс меняется на противоположный. Уравнения, описывающие переходный процесс будут иметь такой же вид, как для пуска двигателя, только wнач нужно принять равной 0, Мнач=-Мп и wс=-wс`,т.е.
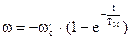 ;
; 
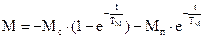
Здесь Мп- пусковой момент.
Время реверса  . При переходе скорости через 0 динамический момент Мдин скачком изменяется от значения Мдин=-(Мп+Мс) до Мдин=-(Мп-Мс) , что вызывает соответствующее изменение ускорения и в кривых w=f(t) и M=f(t) появляется излом.
. При переходе скорости через 0 динамический момент Мдин скачком изменяется от значения Мдин=-(Мп+Мс) до Мдин=-(Мп-Мс) , что вызывает соответствующее изменение ускорения и в кривых w=f(t) и M=f(t) появляется излом.
При динамическом торможении законы изменения w и М описываются теми же уравнениями, что и для реверса, т.е.
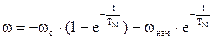 ;
; 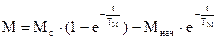 , где wс- установившаяся
, где wс- установившаяся
скорость, определяемая точкой пересечения механической характеристики динамического торможения и вертикали Мc =const.
В случае активного Мс точка “B”, соответствующая установившейся скорости wс2, относится к случаю, когда этот момент в начале процесса является тормозным, что имеет место, например, при подъеме груза, а т. “c” с установившейся скоростью wс1- к случаю, когда этот момент является движущим, например, при спуске груза (рис.а).
 |
В случае торможения при подъеме груза под действием Мс и тормозного момента двигателя привод вначале будет тормозится и остановится, т.к. момент двигателя станет равным 0, но т.к. Мс является активным и будет продолжать действовать в том же направлении, под его действием система будет вращаться в обратную сторону. При этом Мс из момента сопротивления (тормозного) превратится в движущий, а тормозной момент двигателя изменит свой знак и будет продолжать действовать как тормозной. Установившаяся скорость наступит при равенстве момента двигателя и Мс т.е. в т. В. Кривые переходного процесса для этого случая изображены на рис. “б”. Время торможения до w=0 , т.е. до остановки
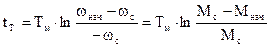
Если активный момент сопротивления в начале торможения был движущим (торможение при спуске груза ), то в начале торможения тормозной момент двигателя (отрезок ED на рис.”а”) больше движущего статического момента и имеет место замедление, сопровождающееся уменьшением тормозного момента двигателя. При скорости wс1 M=Mc, замедление прекращается и наступает установившийся режим тормозного спуска груза со скоростью wс1. В этом случае затормозить систему до остановки путем динамического торможения нельзя (рис.”в”).
При реактивном моменте сопротивления динамическое торможение происходит так же, как  и при подъеме груза. Разница лишь в том, что при w=0 действие реактивного Мс прекратится, и т.к. момент двигателя тоже станет равным 0, система остановится. Соответствующие этому случаю механические характеристики и кривые w=f(t) и М=f(t) изображены на приведенных рис. Процесс будет протекать так, как если бы скорость w стремилась стать равной-wс , но прекратится при w=0. Поэтому соответствующие отрезки кривых на графике изображены пунктиром.
и при подъеме груза. Разница лишь в том, что при w=0 действие реактивного Мс прекратится, и т.к. момент двигателя тоже станет равным 0, система остановится. Соответствующие этому случаю механические характеристики и кривые w=f(t) и М=f(t) изображены на приведенных рис. Процесс будет протекать так, как если бы скорость w стремилась стать равной-wс , но прекратится при w=0. Поэтому соответствующие отрезки кривых на графике изображены пунктиром.
В заключение следует отметить, что процессы пуска и торможения в электроприводах, получающих питание от сети (w =const) отличаются от оптимальных.
Переходные процессы электропривода с линейной механической характеристикой при Мс=f(w)
В случае линейной М от w, т.е. при Мс=кw дифференциальное уравнение, определяющее переходный процесс, имеет вид
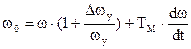 , где
, где
wy- скорость установившегося режима при Мс=Мy ,
Dwy- падение скорости при установившемся режиме .
 Учитывая, что wy+Dwy=w0 и умножая обе части уравнения на
Учитывая, что wy+Dwy=w0 и умножая обе части уравнения на 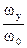 , получим
, получим
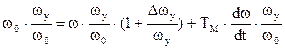
откуда 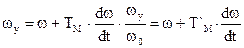 ,где
,где 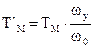
Решение этого уравнения относительно w и М дает законы изменения w , М и I
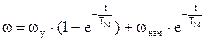 ;
; 

Длительность переходного процесса 
Т`м- это время, за которое электропривод разгонится из неподвижного состояния до wy при постоянном Мпуск.

При Мс=М0+К1w (рис.”a”) и Мс=М0-К1w (рис.”б”) переходный процесс описывается этими же уравнениями, что и при Мс=Кw, но в них 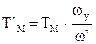
При вентиляторном моменте сопротивления дифференциальное уравнение, отражающее переходный процесс, имеет вид
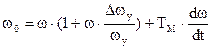
Хотя это уравнение решить можно, однако конечные результаты мало пригодны для практического использования.Поэтому на практике чаще используются графические и графоаналитические методы. Естественно, что такие методы дают лишь приближенные результаты, однако, при тщательном выполнении их точность достаточна для решения практических задач. Правда, такие методы имеют и такой недостаток: они не дают возможности получить общие выводы. Решение может быть найдено лишь для отдельных частных случаев, когда значения всех параметров электропривода известны. Рассмотрим некоторые из них.
Графический метод интегрирования уравнения движения (метод пропорций)
Сущность этого метода заключается в замене бесконечно малых приращений скорости и времени малыми, но конечными приращениями Dw и Dt.
Действительные кривые w=f(M) и w=f(Mс) заменяются ступенчатыми. На каждом участке значения М и Мс или их алгебраическая сумма принимаются постоянными и равными их среднему значению на этом участке, т.е. предполагается, что в уравнение движения электропривода подставляются средние значения М и Мс.
В соответствие с этим уравнение движения можно представить, в виде
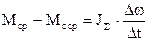
Считая, что в интервале времени Dt разность Мср-Мс.ср остается величиной постоянной; получим пропорцию 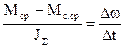
Для графического построения все входящие в нее величины должны изображаться в соответствующих масштабах. Они связаны между собой соотношением 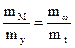
Пропорция, выраженная в отрезках на осях, будет иметь вид

Произвольно выбираются 3 масштабных коэффициента (обычно mM, mw, mt).
Этот метод сводится к графическому построению кривых w=f(t) и M=f(t) и определению  времени переходного процесса. Рассмотрим этот метод на примере пуска электропривода вентилятора. Во втором квадранте изображается механическая характеристика двигателя (в данном случае линейная) и механическая характеристика вентилятора – кривая Мс. Вычтя графически из кривой М=f(w) кривую Мс=f(w), получим кривую динамического момента Мдин=М-Мс. Ее делим на участки, на каждом из которых принимаем Мдин=const т.е. кривую Мдин заменяем ступенчатой (см. график) линией с участками М-Мс=const . Точность конечных результатов тем выше, чем на большее число участков разбита кривая Мдин.
времени переходного процесса. Рассмотрим этот метод на примере пуска электропривода вентилятора. Во втором квадранте изображается механическая характеристика двигателя (в данном случае линейная) и механическая характеристика вентилятора – кривая Мс. Вычтя графически из кривой М=f(w) кривую Мс=f(w), получим кривую динамического момента Мдин=М-Мс. Ее делим на участки, на каждом из которых принимаем Мдин=const т.е. кривую Мдин заменяем ступенчатой (см. график) линией с участками М-Мс=const . Точность конечных результатов тем выше, чем на большее число участков разбита кривая Мдин.
Деление нужно выполнить так, чтобы площадки, создаваемые ступенчатой линией по обе стороны от исходной кривой, были равновеликими. Полученные на отдельных участках значения средних динамических моментов оа1, оа2 и т.д. откладываются на оси ординат в виде отрезков ов1, ов2 и т.д. Полученные т.о. точки в1, в2,в3 и т.д. соединяются наклонными прямыми с т. А, находящейся на оси абсцисс на расстоянии ОА, пропорциональном величине  .
.
Затем из начала координат проводится ОС1, параллельно АВ1 до пересечения в т.С1 с прямой, являющейся продолжением верхнего основания прямоугольника первой ступеньки. Точка С1 является точкой искомой кривой w=f(t) и определяет величину Dw1. Действительно, отрезок ОС1 характеризует закон изменения w на первом участке от w=0 до w=Dw1, что следует из подобия треугольников АОВ1 и Оt1C1.

Т.к.  ;
;  ;
;  ; то
; то 
Проведя аналогичное построение для всех, последующих участков, найдем кривую w=f(t) и искомое время пуска электропривода. Взамен ломанной кривой скорости можно провести плавную кривую.
Для построения кривой М=f(t) необходимо для каждого момента времени t1,t2, и т.д. найти значения момента двигателя (отрезки измеряются от оси ординат до кривой М=f(w) при соответствующем приращении Dw). Например в момент времени t=0 , w=0- это отрезок ОВ. В момент времени t1, w=Dw1- это отрезок ДE и т.д. Откладывая по вертикали от оси абсцисс при каждом моменте времени t1, t2 и т.д. значения найденных графически моментов двигателя, получим точки d, d1, d2, и т.д. , соединяя которые плавной кривой, найдем зависимость M=f(t) в переходном процессе пуска. Изложенный метод применим и для расчета переходного процесса при торможении электропривода. Нужно только иметь в виду, что при торможении динамический момент обычно равен сумме М и Мс и имеет отрицательный знак. Поэтому при построении средние значения Мдин откладываются по оси ординат вниз от т.0.
Графоаналитический метод интегрирования уравнения движения (метод последовательных интервалов)
Метод применяется при нелинейных механических характеристиках двигателя и механизма. Для расчета нужно иметь эти механические характеристики. Имея их, строится кривая динамического момента, как и в методе пропорций.
Пусть кривая момента двигателя задана в виде ломанной линии (пуск в несколько ступеней), а кривая статического момента – в виде пунктирной кривой (см. график). Задаваясь  последовательно приращениями скорости Dw1, Dw2 и т.д. находят среднее значение Мдин.ср. для каждого участка. Иначе говоря, кривая динамического момента (она здесь неизображена) делится на ряд участков, на каждом из которых Мдин. считается постоянным и равным среднему значению.
последовательно приращениями скорости Dw1, Dw2 и т.д. находят среднее значение Мдин.ср. для каждого участка. Иначе говоря, кривая динамического момента (она здесь неизображена) делится на ряд участков, на каждом из которых Мдин. считается постоянным и равным среднему значению.
Полученные значения Мдин.ср. подставляются в формулу

И вычисляется время 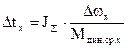 для каждого участка приращения w.
для каждого участка приращения w.
Обычно все расчеты сводятся в таблицу, на основании которой строится кривая w=f(t) и аналогично изложенному ранее, кривая М=f(t).
Уравнения переходных процессов электропривода с линейной механической характеристикой при w0=f(t) и Mc=const.
При пуске электропривода включением его в сеть на полное напряжение U=const и f1=const переходные процессы протекают при скачке напряжения, или как говорят, скачке управляющего воздействия, когда w0=const. Для ограничения бросков тока и момента в якорную или роторную цепь двигателя приходится вводить добавочное сопротивление. Переходные процессы при этом будут далеки от оптимальных. При питании двигателя от преобразователя напряжения или частоты ( в замкнутых системах) можно получить переходные процессы, близкие к оптимальным, путем плавного изменения управляющего воздействия. Они протекают в этом случае при w0=f(t). При этом ограничивается темп нарастания управляющего воздействия путем ограничения ускорения e0 Т.о. переходные процессы протекают в этом случае при U=var или f=var.
Проанализируем переходные процессы при линейном изменении управляющего воздействия w0 во времени, т.е. при линейном изменении U или f1, при котором w0=w0 нач+e0t.
Исходными дифференциальными уравнениями для получения расчетных соотношений являются ранее полученные уравнения
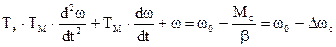

При соотношении постоянных времени  величиной Тэ можно пренебречь и уравнение, определяющее закон изменения w, будет иметь вид
величиной Тэ можно пренебречь и уравнение, определяющее закон изменения w, будет иметь вид

Правая часть этого уравнения – частное решение, соответствующее установившемуся режиму, когда все свободные составляющие затухнут. Для этого режима w=a+bt, где а и b – неопределенные коэффициенты , находимые из начальных условий. Имея в виду, что  , получим при t=0
, получим при t=0 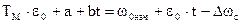
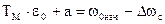 Отсюда
Отсюда 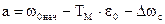
Общее решение дифференциального уравнения относительно w
 или
или
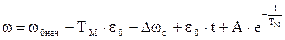
При t=0 w=wнач , следовательно 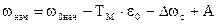 ,откуда
,откуда
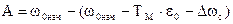 .
.
Окончательно закон изменения скорости

Закон изменения момента в переходном режиме находится аналогично
 .отсюда
.отсюда
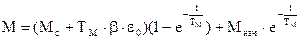
Используя эти выражения, исследуем переходные процессы при различных режимах и различных по характеру моментах сопротивления.
Переходный процесс пуска электропривода с линейной механической характеристикой при реактивном моменте сопротивления и w0=f(t)
Исходными уравнениями для анализа переходного процесса являются
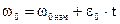


Изобразим механические характеристики, на которых электропривод работает в процессе  пуска, а рядом будут изображаться кривые переходного процесса. Процесс пуска разбивается на три этапа. На первом этапе двигатель неподвижен (w=0), а момент его нарастает по линейному закону
пуска, а рядом будут изображаться кривые переходного процесса. Процесс пуска разбивается на три этапа. На первом этапе двигатель неподвижен (w=0), а момент его нарастает по линейному закону

т.к. w0 нач=0
Время запаздывания 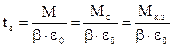
По достижении моментом двигателя значения, равного Мс, двигатель приходит во вращение и начинается второй этап (II), который закончится, когда w0 перестанет изменяться, т.е. станет равной w0=const. Начальные условия для второго этапа : wнач=0 ; w0 нач=Dwс ; Mнач=Мс.
Законы изменения w и М получим, подставив начальные условия в исходные уравнения

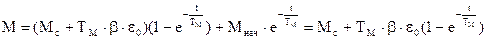
Кривые отражающие процесс на этом этапе изображены на графике (начало координат переносится при этом в т. tз и отсчет времени начинается с момента tз.).
В конце второго этапа (t=t0) двигатель выходит на характеристику, соответствующую w0=const. До этого он последовательно переходит с одной характеристики на другую, каждой из которых соответствует своя w0. Зависимости w=f(t) и М=f(t) позволяют построить фазовую траекторию, т.е. динамическую характеристику (см.график).
На третьем этапе (III) двигатель работает при неизменном U (неизменной частоте f1) при w0=const. Происходит дотягивание до скорости, соответствующей установившемуся режиму в т.А. На этом этапе законы изменения w и М описываются уравнениями соответствующими w0=const, т.е. постоянству управляющего воздействия (постоянству U сети или постоянству частоты f1


Начало координат при этом надо перенести в т. t0, т.е. время на этом этапе отсчитывается от t0. Общее время переходного процесса tпп=tз+t0+3TM.
Переходный процесс электропривода с линейной механической характеристикой при реверсе и w0=f(t)
При активном Мс переходный процесс в случае плавного изменения управляющего воздействия (U1 или f1) при котором w0 изменяется по закону
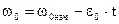
исходными уравнениями для анализа переходного процесса являются те же ,что и при реактивном Мс. Считаем, что w0 изменяется от w0 ном до -w0 ном. Реверс разбивается на два этапа. Первый этап заканчивается когда w0 станет равной -w0 ном и двигатель выходит на характеристику, соответствующую этой скорости.
 Подставляя в исходные уравнения значения w0 нач =w0 ном, wнач =wс, Мнач =Мс и учитывая, что ускорение e0 при снижении скорости отрицательно, получим для первого этапа реверса законы изменения w и М
Подставляя в исходные уравнения значения w0 нач =w0 ном, wнач =wс, Мнач =Мс и учитывая, что ускорение e0 при снижении скорости отрицательно, получим для первого этапа реверса законы изменения w и М
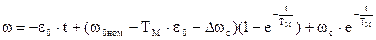
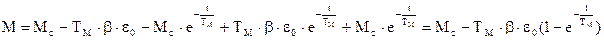
В зависимости от соотношения Мс, e0 и Тм суммарный перепад скорости
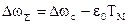
 может быть больше, равен или меньше 0. Если
может быть больше, равен или меньше 0. Если 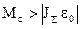 , двигатель в процессе снижения скорости продолжает работать в двигательном режиме, Dwс>0, а при изменении знака w , т.е. изменении направления вращения, переходит в тормозной режим с w>w0.
, двигатель в процессе снижения скорости продолжает работать в двигательном режиме, Dwс>0, а при изменении знака w , т.е. изменении направления вращения, переходит в тормозной режим с w>w0.
При  двигатель при снижении скорости работает в тормозном режиме с w>w0 , а при разгоне в противоположном направлении переходит в двигательный режим (пунктирная кривая на графике ).
двигатель при снижении скорости работает в тормозном режиме с w>w0 , а при разгоне в противоположном направлении переходит в двигательный режим (пунктирная кривая на графике ).
На втором (II) этапе процесс протекает при w0 =-w0 ном=const и описывается уравнениями как при питании от сети с неизменным напряжением (частотой) . Длительность этого этапа
~ 3ТМ. Происходит дотягивание до скорости -wс.
Процесс реверса при реактивном Мс рассмотрим на примере электропривода с ДНВ при линейном изменении напряжения на якоре двигателя

В процессе торможения закон движения электропривода тот же, что и при активном Мс. Начальная разность между напряжением Uя=Uн на якоре и ЭДС двигателя Е=КФwс, равная падению напряжения на сопротивлении якорной цепи от тока статической нагрузки JcRяS, уменьшается до значения, равного падению напряжения от установившегося тока при реверсе

 . Ток якоря при этом уменьшается от значения Ic до Iр.уст и затем остается неизменным до w=0. В момент перехода w через 0 Мс изменяет свой знак.
. Ток якоря при этом уменьшается от значения Ic до Iр.уст и затем остается неизменным до w=0. В момент перехода w через 0 Мс изменяет свой знак.
Для того, чтобы начался разгон в противоположную сторону, необходимо, чтобы ток тоже изменил направление на противоположное и увеличился после этого до значения, превышающего 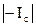 .Поэтому возникает пауза в движении, аналогичная времени запаздывания пр пуске в ход.
.Поэтому возникает пауза в движении, аналогичная времени запаздывания пр пуске в ход.
Во время этой паузы ток нарастает (см. график) по закону

 ; а w=0
; а w=0
Пауза заканчивается, когда ток станет равным –Ic и двигатель начинает вращаться в противоположном направлении . Далее процесс будет протекать аналогично случаю пуска. Время паузы

Если увеличивать темп изменения Uя, т.е. величину 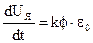 , то вследствие роста динамического тока Iдин=Iс-Iр.уст при торможении ток Iр.уст=Iс-Iдин вначале будет уменьшаться
, то вследствие роста динамического тока Iдин=Iс-Iр.уст при торможении ток Iр.уст=Iс-Iдин вначале будет уменьшаться
до 0 , а затем изменит свой знак. При этом tп уменьшается и при Iр.уст=Iс становится равным 0. Из уравнения движения для этого случая –М-Мс=ISe0 можно определить ускорение e0` соответствующее этому условию
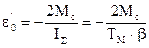
Если 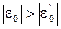 , то процесс изменения w при реверсе является непрерывным, лишь при переходе w через 0 скачком изменяется ускорение . Для рассмотренного случая на левом графике изображена и динамическая характеристика .
, то процесс изменения w при реверсе является непрерывным, лишь при переходе w через 0 скачком изменяется ускорение . Для рассмотренного случая на левом графике изображена и динамическая характеристика .
Рассмотренные переходные процессы позволяют сделать выводы : 1) Задаваемый на входе системы закон изменения скорости w воспроизводится с ошибкой, которая в установившемся переходном процессе складывается из ошибки, равной статическому перепаду скорости Dwс и ошибки, равной динамическому падению
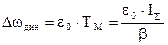 ;
; 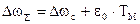
Увеличение b статической механической характеристики влечет за собой соответствующее уменьшение отклонения кривой w=f(t) от кривой w0=f(t) .
2). Закон изменения UЯ для двигателей постоянного тока или частоты f1 для двигателей переменного тока определяет характер изменения w в переходном режиме с тем большей точностью, чем меньше Тм . Этот вывод справедлив не только для случая линейного закона изменения управляющего воздействия, но и, например, для экспоненциального закона. В качестве примера оценим характер изменения ЭДС двигателя, пропорциональной скорости w в переходном процессе пуска двигателя постоянного тока при Мс=0, когда Uя измениться по закону 
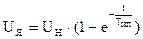 , где Тип – электромагнитная постоянная времени источника питания. Пусть Тип>>Тм . Начальная часть кривой UЯ близка прямой 1, соответствующей неизменному значению
, где Тип – электромагнитная постоянная времени источника питания. Пусть Тип>>Тм . Начальная часть кривой UЯ близка прямой 1, соответствующей неизменному значению  . Если бы UЯ нарастало по линейному закону, ток изменялся бы по закону экспоненты (кривая 2) с постоянной Тм, стремясь к значению Iмакс . Но поскольку темп нарастания UЯ в действительности уменьшается, ток, достигнув значения I``макс при t=tмакс, начнет уменьшаться по закону близкому к закону, определяющему темп изменения напряжения
. Если бы UЯ нарастало по линейному закону, ток изменялся бы по закону экспоненты (кривая 2) с постоянной Тм, стремясь к значению Iмакс . Но поскольку темп нарастания UЯ в действительности уменьшается, ток, достигнув значения I``макс при t=tмакс, начнет уменьшаться по закону близкому к закону, определяющему темп изменения напряжения 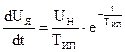 . ЭДС двигателя изменяется по кривой 3 , отличаясь от UЯ в каждый момент времени на величину падения напряжения в цепи якоря при данном токе. Чем меньше ТМ, тем меньше падение напряжения, тем ближе кривая 3 к кривой UЯ.
. ЭДС двигателя изменяется по кривой 3 , отличаясь от UЯ в каждый момент времени на величину падения напряжения в цепи якоря при данном токе. Чем меньше ТМ, тем меньше падение напряжения, тем ближе кривая 3 к кривой UЯ.
Дата добавления: 2015-10-05; просмотров: 1169;
