Свойства смешанного произведения векторов

Определение. Смешанным произведением трех векторов 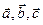называется скалярное произведение векторного произведения первых двух векторов на третий.

Обозначение: 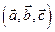, т.е.

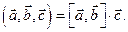
Из этого определения следует, что три вектора компланарны (параллельны одной плоскости) тогда и только тогда, когда их смешанное произведение равно нулю.

Теорема. Смешанное произведение трех векторов равно определителю третьего порядка, строки которого составлены из координат этих векторов, т.е.

,

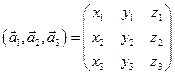где .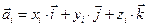

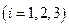Доказательство. Имеем:

= .

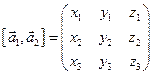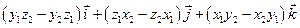Следовательно,

= = .

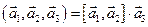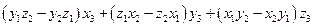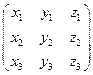Так как

= ,

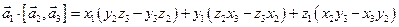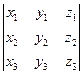то смешанное произведение трех векторов можно определить как скалярное произведение первого вектора на векторное произведение двух других.

Из свойств определителя следует: 1) при циклической перестановке смешанное произведение не меняется, т.е.

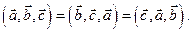
При перестановке любых двух векторов оно меняет только знак, сохраняя абсолютную величину, т.е.

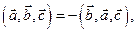
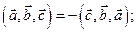
3)необходимым и достаточным условием компланарности трех векторов является равенство нулю определителя из их координат.

Теорема. Модуль смешанного произведения трех векторов равен объему параллелепипеда, построенного на векторах - сомножителях.

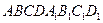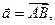
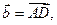
Доказательство. Пусть V - объем параллелепипеда , построенного на векторах 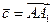. Так как 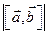равен площади параллелограмма 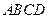, а объем параллелепипеда равен произведению

площади основания на высоту

,

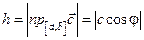то

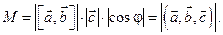
Следствие. Объем пирамиды 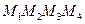определяется формулой:

,

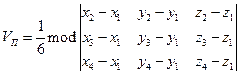где 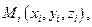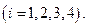Действительно, объем пирамиды равен 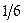объема параллелепипеда, построенного на векторах , , .

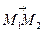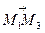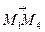Пример. Доказать, что точки 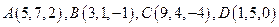лежат в одной плоскости.

Найдем координаты векторов: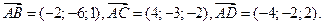

Найдем смешанное произведение полученных векторов:

.

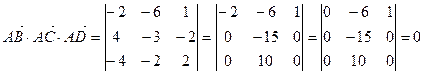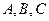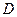Таким образом, полученные выше векторы компланарны, следовательно точки и лежат в одной плоскости.

Пример. Найти объем пирамиды и длину высоты, опущенной на грань 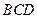, если вершины имеют координаты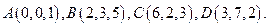

Найдем координаты векторов: .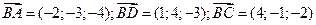

Объем пирамиды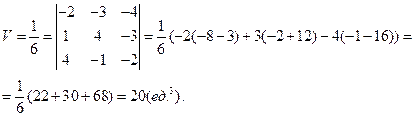

Для нахождения длины высоты пирамиды найдем сначала площадь основания :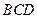

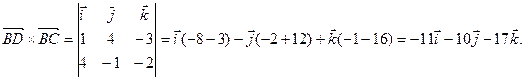
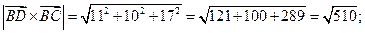
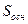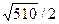= (ед.²).

Так как V = 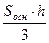; 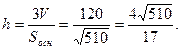(ед.).