Элементы векторной алгебры
Раздел 3. Элементы аналитической геометрии и векторной алгебры
Элементы векторной алгебры
1. Определение вектора. Линейные операции над векторами
Определение. Вектором (на прямой, на плоскости, в пространстве) называется упорядоченная пара точек А, В, или направленный отрезок. Точка А называется началом вектора, точка В - его концом. Вектор, начало и конец которого совпадают, называется нуль-вектором.
Векторы обычно обозначаются или двумя большими буквами со стрелкой или чертой наверху, или малой буквой также со стрелкой или чертой наверху: 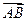 ,
, 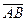 ,
, 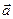 ,
, 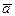 . Первая из двух букв означает начало вектора, вторая - его конец.
. Первая из двух букв означает начало вектора, вторая - его конец.
Определение. Длина отрезка 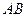 называется длиной или модулем вектора и обозначается
называется длиной или модулем вектора и обозначается 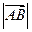 или
или 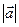 .
.
Определение. Два ненулевых вектора 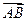 и
и 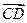 называются коллинеарными, если они лежат на одной или на параллельных прямых. Обозначение:
называются коллинеарными, если они лежат на одной или на параллельных прямых. Обозначение: 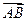 ïê
ïê 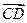 .
.
Определение. Коллинеарные векторы называются одинаково (противоположно) направленными, если (в случае принадлежности разным прямым) их концы лежат по одну сторону (по разные стороны) от прямой, соединяющей их начала, а в случае принадлежности одной прямой, если из двух лучей, определяемых этими векторами, один содержится (не содержится) в другом. Обозначение 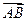
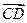 (
( 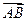 ¯
¯ 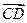 ).
).
Определение. Два вектора 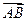 и
и 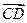 называются равными, если они одинаково направлены и имеют равные длины, т.е. если
называются равными, если они одинаково направлены и имеют равные длины, т.е. если 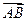
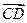 , ï
, ï 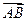 ï=ï
ï=ï 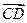 ï.
ï.
Легко проверить выполнение трех аксиом отношения эквивалентности для понятия равенства векторов:
1) 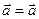 , 2)
, 2) 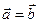
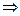
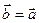 , 3)
, 3) 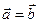 и
и 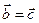
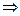
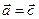 .
.
Отложить вектор 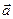 от точки М -значит построить вектор
от точки М -значит построить вектор 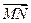 , равный вектору
, равный вектору 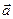 .
.
Определение. Суммой 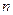 векторов
векторов 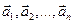 называется вектор
называется вектор 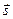 , получающийся следующим построением: от произвольной точки А (прямой, плоскости, пространства) откладываем первый вектор
, получающийся следующим построением: от произвольной точки А (прямой, плоскости, пространства) откладываем первый вектор 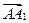 , равный вектору
, равный вектору 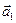 , от конца
, от конца 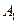 вектора
вектора 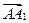 откладываем второй вектор
откладываем второй вектор 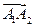 , равный вектору
, равный вектору 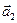 и т.д.: суммой
и т.д.: суммой 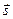 является вектор, соединяющий начальную точку А с концом
является вектор, соединяющий начальную точку А с концом 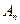 последнего отложенного вектора
последнего отложенного вектора 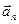 .
.
Обозначение:
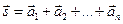 .
.
Для двух векторов 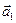 и
и 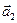 указанное правило сводится к правилу треугольника, из которого следует правило параллелограмма.
указанное правило сводится к правилу треугольника, из которого следует правило параллелограмма.
Операция сложения векторов ассоциативна и коммутативна, так как при любом порядке откладывания векторов - слагаемых мы придем к тому же самому результату.
Определение. Произведением действительного ненулевого числа l на ненулевой вектор 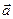 называется вектор, обозначаемый
называется вектор, обозначаемый 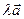 или
или 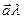 , удовлетворяющий следующим трем условиям:
, удовлетворяющий следующим трем условиям:
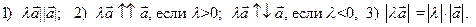
Произведение любого вектора на нуль и нуль-вектора на любое число, по определению, есть нуль-вектор, т.е.
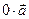 =
= 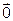 ,
, 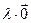 =
= 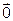 .
.
Справедливы следующие свойства умножения вектора на число:
1) 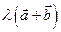 =l
=l 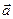 +l
+l 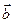 ; 2)
; 2) 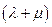
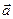 =l
=l 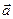 +m
+m 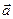 ; 3) l
; 3) l 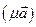 =
= 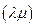
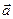 ,
,
справедливые для любых чисел 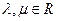 и любых векторов
и любых векторов 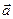 ,
, 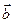 .
.
Дата добавления: 2015-09-29; просмотров: 814;
