ЯВЛЕНИЕ И ЗАКОН САМОИНДУКЦИИ
Явление возникновения э.д.с. в том же проводнике, по которому течёт переменный ток, называют самоиндукцией, а саму э.д.с. ¾ э.д.с. самоиндукции. Возникновение э.д.с. самоиндукции объясняется следующим. Переменный ток, проходящий по проводнику, порождает вокруг себя переменное магнитное поле, которое, в свою очередь, создаёт магнитный поток, изменяющийся со временем, через площадь, ограниченную проводником.
Согласно явлению электромагнитной индукции, это изменение магнитного потока и приводит к появлению э.д.с. Значение э.д.с. самоиндукции найдём, подставляя выражение (1) в закон электромагнитной индукции (см. (14) лекцию №9) и полагая, что L = const: 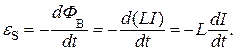 Итак,
Итак,
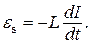 (4)
(4)
Итак, э.д.с. самоиндукции в проводнике пропорциональна скорости изменения силы тока, текущего по нему.
Под действием э.д.с. самоиндукции создаётся индукционный ток, называемый током самоиндукции.
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
                 Рис. 1 Рис. 1
|
Пусть в электрической цепи (рис. 1) протекает постоянный ток силой I. Если отключить источник тока и замкнуть цепь (переключатель П перевести в положение 2), то в ней некоторое время будет течь убывающий ток, обусловленный э.д.с. самоиндукции es, равной 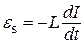 . Элементарная работа, совершаемая э.д.с. самоиндукции по переносу по цепи элементарного заряда dq = I·dt, равна
. Элементарная работа, совершаемая э.д.с. самоиндукции по переносу по цепи элементарного заряда dq = I·dt, равна 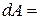
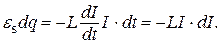 Сила тока изменяется от I до 0. Поэтому, интегрируя это выражение в указанных пределах, получаем работу, совершаемую э.д.с. самоиндукции за время, в течение которого происходит исчезновение магнитного поля:
Сила тока изменяется от I до 0. Поэтому, интегрируя это выражение в указанных пределах, получаем работу, совершаемую э.д.с. самоиндукции за время, в течение которого происходит исчезновение магнитного поля: 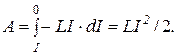 Совершение этой работы сопровождается нагреванием проводника и окружающей среды и исчезновением магнитного поля, которое первоначально существовало вокруг проводника. Поскольку никаких других изменений в окружающей среде не происходит, то можно заключить, что магнитное поле обладает энергией, за счёт которой и совершается работа. Итак, энергия магнитного поля, существующего вокруг проводников с током, равна
Совершение этой работы сопровождается нагреванием проводника и окружающей среды и исчезновением магнитного поля, которое первоначально существовало вокруг проводника. Поскольку никаких других изменений в окружающей среде не происходит, то можно заключить, что магнитное поле обладает энергией, за счёт которой и совершается работа. Итак, энергия магнитного поля, существующего вокруг проводников с током, равна
WB= LI2/ 2. (5)
Выразим энергию магнитного поля через величины, характеризующие само поле. Проделаем это на примере соленоида. Из формул (2) и (3) I = B/(mm0n) и L =mm0n2V. Подставляя эти выражения в (5), получаем, что
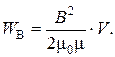 (6)
(6)
Магнитное поле внутри соленоида однородное ( 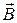 = const). Поэтому объёмная плотность энергии wBмагнитного поля, т.е. энергия единицы объёма поля, внутри соленоида равна
= const). Поэтому объёмная плотность энергии wBмагнитного поля, т.е. энергия единицы объёма поля, внутри соленоида равна
wB = WB/V = B2 /(2mm0). (7)
Эта формула справедлива и в случае неоднородных статических и переменных магнитных полей.
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
Из закона Фарадея для электромагнитной индукции
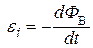 (8)
(8)
следует, что при всяком изменении магнитного потока, пронизывающего площадь, охватываемую проводником, в нём возникает э.д.с. индукции, под действием которой в проводнике появляется индукционный ток, если проводник замкнутый.
Для объяснения э.д.с. индукции Максвелл выдвинул гипотезу, что переменное магнитное поле создаёт в окружающем пространстве электрическое поле. Это поле действует на свободные заряды проводника, приводя их в упорядоченное движение, т.е. создавая индукционный ток. Таким образом, замкнутый проводящий контур является своеобразным индикатором, с помощью которого и обнаруживается данное электрическое поле. Обозначим напряжённость этого поля через 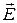 . Тогда э.д.с. индукции
. Тогда э.д.с. индукции
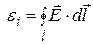 . (9)
. (9)
(см. понятие э.д.с. источника). Объединяя соотношения (8) и (9), получаем
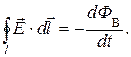 (10)
(10)
Из электростатики известно, что циркуляция напряжённости 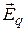 электростатического поля равна нулю, т.е.
электростатического поля равна нулю, т.е. 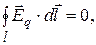 где
где 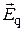 — напряжённость электростатического поля. Это соотношение является условием потенциальности электростатического поля. Однако из (10) следует, что
— напряжённость электростатического поля. Это соотношение является условием потенциальности электростатического поля. Однако из (10) следует, что 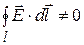 , т.е. электрическое поле, возбуждаемое изменяющимся со временем магнитным полем, является вихревым (не потенциальным).
, т.е. электрическое поле, возбуждаемое изменяющимся со временем магнитным полем, является вихревым (не потенциальным).
Следует отметить, что линии напряжённости электростатического поля начинаются и заканчиваются на зарядах, создающих поле, а линии напряжённости вихревого электрического поля всегда замкнутые.
ТОК СМЕЩЕНИЯ
Как указывалось, Максвелл высказал гипотезу, что переменное магнитное поле создаёт вихревое электрическое поле. Он сделал и обратное предположение: переменное электрическое поле должно вызывать возникновение магнитного поля. В дальнейшем эти обе гипотезы получили экспериментальное подтверждение в опытах Герца. Появление магнитного поля при изменении электрического поля можно трактовать так, как будто бы в пространстве возникает электрический ток. Этот ток был назван Максвеллом током смещения. Ток смещения в отличие от тока проводимости в металлах не связан с движением электрических зарядов, а обусловлен переменным электрическим полем. В действительности никакого тока нет, а есть лишь изменяющееся со временем электрическое поле, которое и создаёт магнитное поле. Однако использование этого термина удобно.
Выясним, от чего зависит ток смещения на простом примере. Рассмотрим плоский конденсатор, на обкладках которого имеются заряды q противоположного знака, равномерно распределённые по обкладкам с поверхностной плотностью, равной s = q/S, где S — площадь обкладки. Внутри конденсатора возникает электрическое поле. Напряжённость этого поля равна
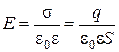 . (11)
. (11)
|
Замкнём обкладки конденсатора проводником (рис. 2). Это приводит к возникновению тока проводимости в проводнике, приводящего к уменьшению заряда на обкладках конденсатора, следовательно, и к ослаблению электрического поля внутри конденсатора. Изменение электрического поля вызывает появление магнитного поля между пластинами конденсатора, обусловленного как бы током смещения силой Icм, текущего внутри конденсатора. Сила этого тока должна равняться силе тока проводимости Iпр, поскольку электрическая цепь не имеет разветвлений. Поэтому Icм = Iпр. Силу тока проводимости находим по формуле 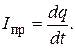 Подставляя в это выражение q, найденное из (11), и вынося постоянные за знак производной, получаем силу тока смещения:
Подставляя в это выражение q, найденное из (11), и вынося постоянные за знак производной, получаем силу тока смещения: 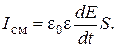 Плотность тока смещения будет равна
Плотность тока смещения будет равна
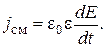 (12)
(12)
В общем случае напряжённость электрического поля может зависеть от координат и времени. Поэтому в выражении (36.2) производную 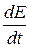 надо заменить частной производной
надо заменить частной производной 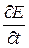 . Тогда
. Тогда
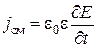 (13)
(13)
и сила тока смещения через площадку S, перпендикулярную к направлению этого тока, равна
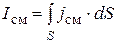 . (14)
. (14)
Ток смещения может возникать не только в вакууме или диэлектрике, но и в проводниках, по которым течёт переменный ток. Однако в этом случае он пренебрежимо мал по сравнению с током проводимости.
Максвелл ввёл понятие полного тока. Сила I полного тока равна сумме сил Iпри Iсмтоков проводимости и смещения, т.е. I = Iпр + Iсм. Используя (14), получаем:
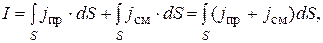 (15)
(15)
где S ¾ площадь поперечного сечения проводника.
УРАВНЕНИЯ МАКСВЕЛЛА
Введение двух гипотез о существовании вихревого электрического поля и тока смещения позволили Максвеллу создать единую теорию электромагнетизма. В основе этой теории находятся четыре уравнения, названные уравнениями Максвелла, которые играют в учении об электромагнетизме такую же роль, как законы Ньютона в классической механике. Рассмотрим эти уравнения.
1. Первое уравнение.Согласно (10), циркуляция напряжённости вихревого электрического поля равна
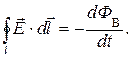 (16)
(16)
Но 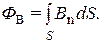 Тогда
Тогда 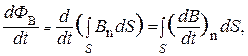 где (
где ( 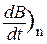 — проекция производной по времени индукции
— проекция производной по времени индукции 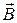 магнитного поля на направление нормали
магнитного поля на направление нормали 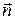 к площади контура. Поскольку в общем случае индукция магнитного поля зависит от координат и времени, то
к площади контура. Поскольку в общем случае индукция магнитного поля зависит от координат и времени, то 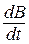 надо заменить частной производной
надо заменить частной производной 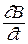 . С учётом этого уравнение (16) запишется
. С учётом этого уравнение (16) запишется
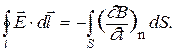 (17)
(17)
Из этого уравнения следует, что источником электрического поля является изменяющееся со временем магнитное поле.
2. Второе уравнение. Максвелл обобщил закон полного тока, введя в её правую часть полный ток 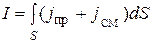 , где S ¾ площадь замкнутого контура длиною l. Учитывая это, закон полного тока запишется
, где S ¾ площадь замкнутого контура длиною l. Учитывая это, закон полного тока запишется
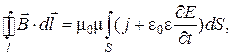 (18)
(18)
поскольку 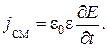 Это уравнение показывает, что магнитное поле может создаваться как движущимися зарядами (электрическим током), так и переменным электрическим полем.
Это уравнение показывает, что магнитное поле может создаваться как движущимися зарядами (электрическим током), так и переменным электрическим полем.
3. В качестве третьегоичетвертого уравненийМаксвелл взял теорему Гаусса для электростатического и магнитного полей
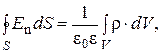 (19)
(19) 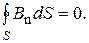 (20)
(20)
Соотношение (19) свидетельствует о том, что линии напряжённости электростатического поля начинаются и кончаются на электрических зарядах, а из (20) следует, что линии магнитной индукции всегда замкнуты, т.е. в природе не существует магнитных зарядов. Необходимо отметить, что нумерация уравнений Максвелла произвольная.
Из уравнений (17) и (18) вытекает, что переменное магнитное поле всегда связано с создаваемым им электрическим полем, и наоборот, переменное электрическое поле связано с создаваемым им магнитным полем. Таким образом, эти поля взаимосвязаны и образуют единое электромагнитное поле. Поэтому отдельное рассмотрение электрических и магнитных полей носит относительный характер. Так, например, если электрическое поле создаётся неподвижными зарядами в одной системе отсчёта, то относительно другой они могут двигаться и, следовательно, порождают одновременно и электрическое и магнитное поля. Уравнения Максвелла являются основой единой теории электрических и магнитных явлений.
Дата добавления: 2015-09-29; просмотров: 1003;
