Анализ комбинационных устройств (без памяти)

Комбинационные устройства — цифровые устройства, выходные сигналы которых зависят только от входных сигналов, действующих в текущий момент времени, и не зависят от предыдущего внутреннего состояния, предше­ствующих входных сигналов. Другими словами, комби­национные устройства — это устройства без памяти. Их можно представить в виде многомерного n, т — многопо­люсника (рис. 1.8).

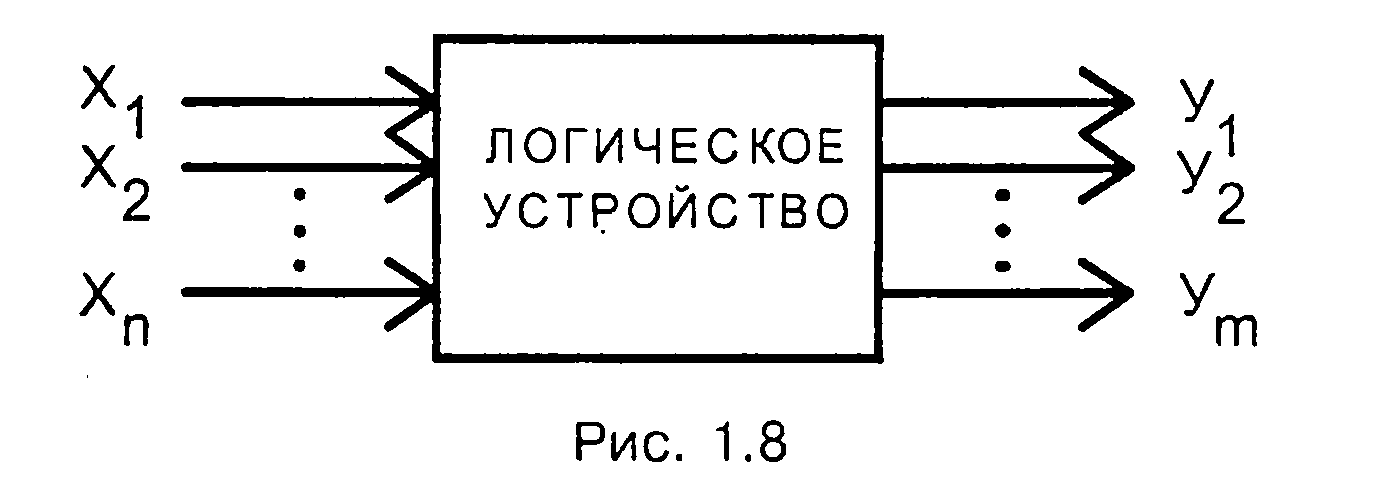
Условия функционирования комбинационного устрой­ства можно представить в виде системы логических функ­ций, называемых функциями выходов

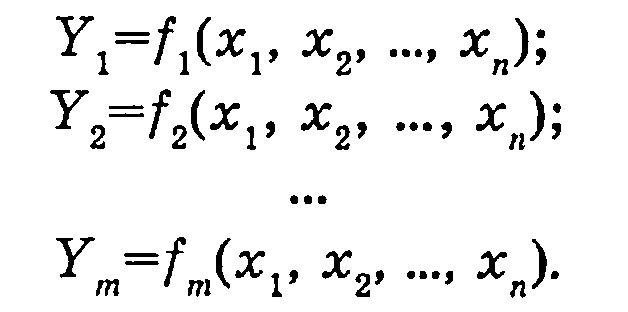
Задача анализа условий функционирования сводится к определению всех функций выхода дискретного устрой­ства по известной принципиальной схеме реального уст­ройства. Результат анализа представляется в виде функ­ций алгебры логики и таблицы истинности. Другими сло­вами, необходимо установить функциональную зависи­мость между входными переменными х₁, х₂,... х_n комбинационного устройства и значениями выходных сигналов y_1, у₂,...у_т в виде формул алгебры логики или таблиц истинности.

Анализ комбинационного устройства целесообразно проводить в следующей последовательности.

1. На функциональной схеме выходы всех логических элементов (ЛЭ) обозначить символами промежуточных переменных.

2. Определить и записать функции непосредственных связей, устанавливающие зависимости выхода каждого ЛЭ от его входов на основе элементарных логических функций.

3. Путем подстановок исключить все внутренние пере­менные. Получить зависимости выходов комбинационно­го устройства у₁,..., у_т от его входов х₁,..., х_п, использова­нием тождеств и соотношений алгебры логики.

4. Составить таблицу истинности.

5. Представить результаты анализа в удобной для пользователя форме.

Последний пятый пункт алгоритма анализа в общем случае уже является переходом к задаче синтеза комбина­ционного устройства.

Приведем пример анализа комбинационного устрой­ства без памяти (рис. 1.9). Оно содержит элементы НЕ (DD1, DD2), И (DD3, DD4), ИЛИ (DD5), ИЛИ-HE (DD6).

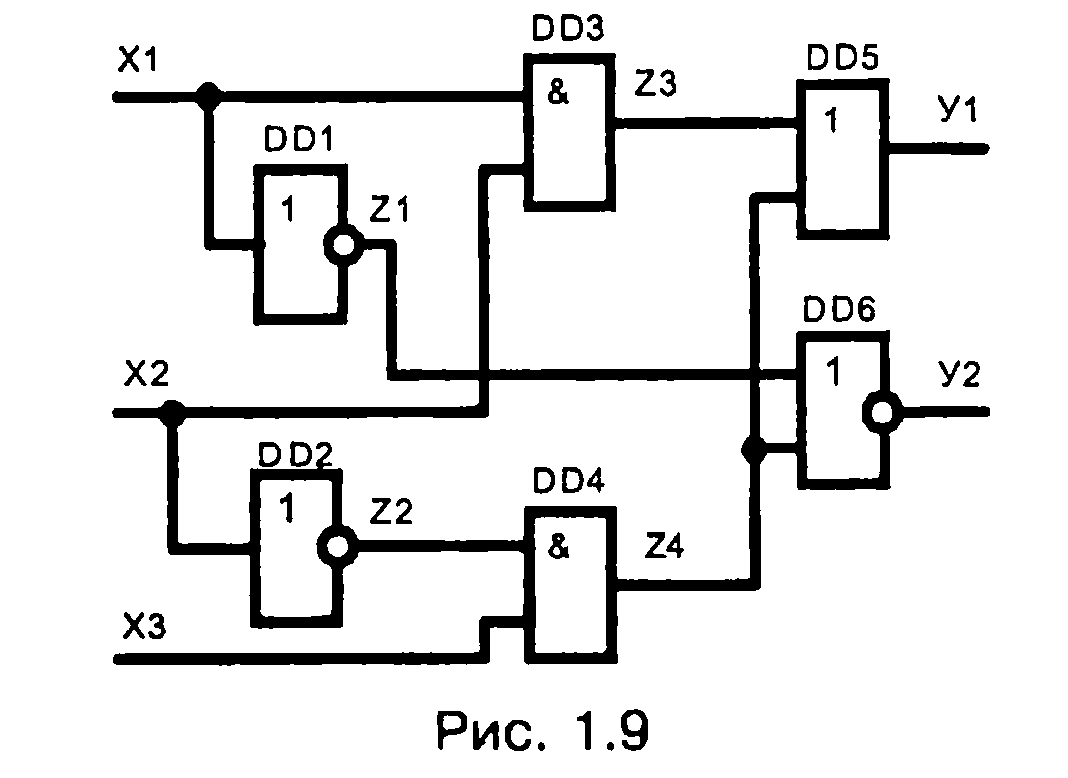
Установим промежуточные переменные z₁, z₂, z₃, z₄ и запи­шем функции связи входов и выходов для каждого ЛЭ.

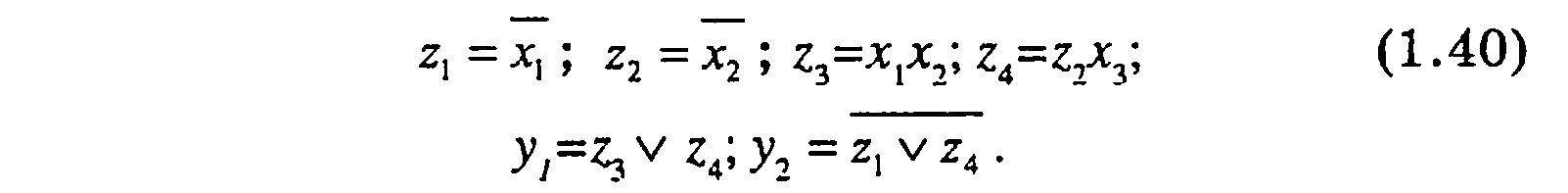исключим внутренние промежуточные переменные

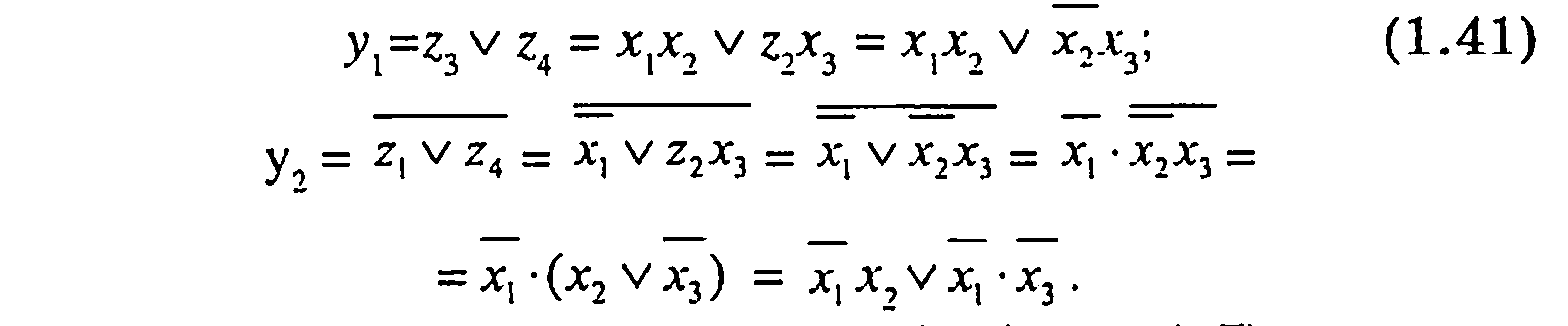
Составим таблицу истинности (таблица 1.7)

Таблицы истинности могут быть записаны в других фор­мах, которые могут оказаться более удобными в различных случаях: карты Вейча, карты Карно и т. д. Например, при записи таблицы истинности в виде карты Карно аргументы функции (входные переменные) делятся на две группы. Ком­бинации значений аргументов одной группы приписывают­ся столбцам таблицы, комбинации значений аргументов дру­гой группы — строкам таблицы. Столбцы и строки обозна­чаются комбинациями, соответствующими последовательно­сти чисел в коде Грея. В коде Грея переход от одной комби­нации к другой соседней сопровождается изменением логи­ческой переменной только в одном разряде.

В двоичном коде переход от 1 к 2 сопровождается измене­нием 01—>10 логической переменной сразу в двух разрядах.

Таблицы 1.9 и 1.10 показывают карты Карно для фун­кций трех и четырех переменных.

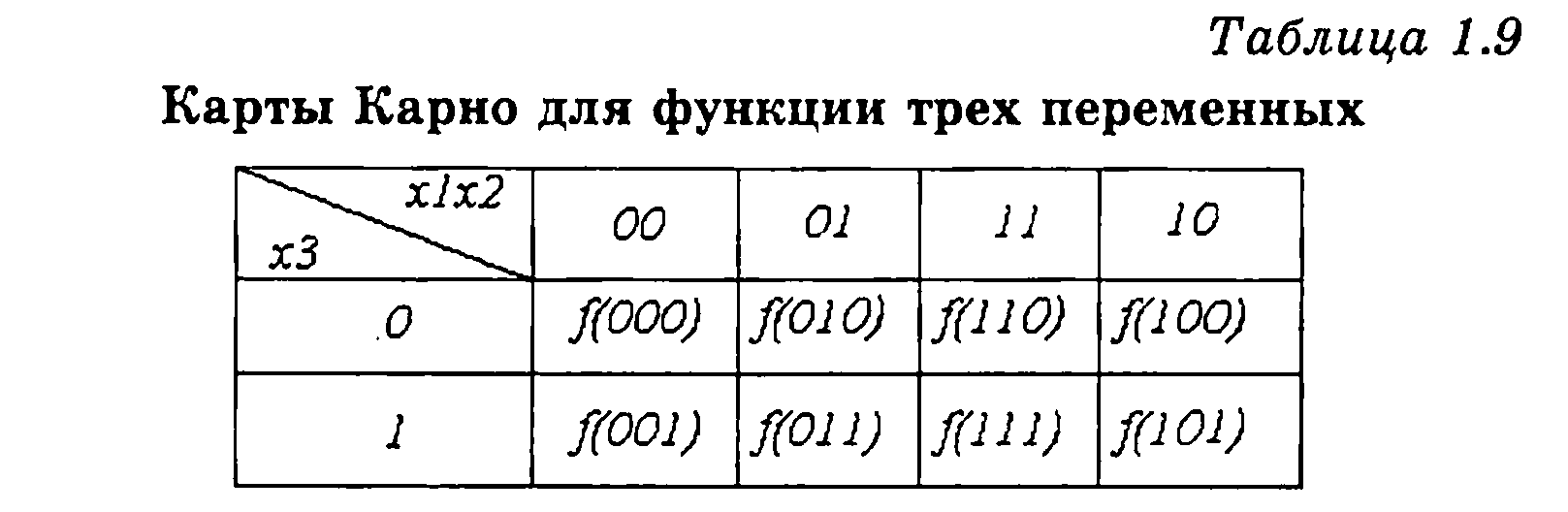
При заполнении карты Карно в ее клетки заносятся значения функции f(x), которые соответствуют набору переменных на пересечении столбца и строки. Запишем пример карты Карно для выхода y₁ (Таблица 1.11).

Единичные значения функции у₁ соответствуют набо­рам х₁х₂х₃ = 110, 001, 101, 111.

Представленный алгоритм анализа справедлив при следующих допущениях:

1. переход логического устройства из одного состояния в другое происходит скачкообразно (не учитывается крутизна переднего и заднего фронта сигналов);

2. изменение сигналов в различных участках схемы происходит одновременно (не учитываются задерж­ки в различных элементах схемы).

Ранее в п. 1.1. отмечались три модели логических ус­тройств, учитывающие технические особенности логичес­ких элементов:

1) логическая модель;

2) модель с временными задержками;

3) модель с учетом электрических параметров и харак­теристик.

Для алгоритма анализа первой логической модели до­статочно только знания соотношений алгебры логики. Во второй модели учитываются временные задержки логи­ческих элементов. Иначе в результате могут возникнуть ситуации, приводящие к ложным срабатываниям. Расче­ты по третьей модели являются достаточно сложными, требуют анализа входных и выходных токов каждого ЛЭ. В результате этих расчетов может выясниться, что требу­ется применение микросхем с более мощными выходами либо включение дополнительных элементов.

Причиной задержек в ЛЭ являются переходные процес­сы. Переходным процессом называют функционирование дискретного устройства в течение интервала времени, не­посредственного следующего за моментом изменения сиг­налов в схеме.

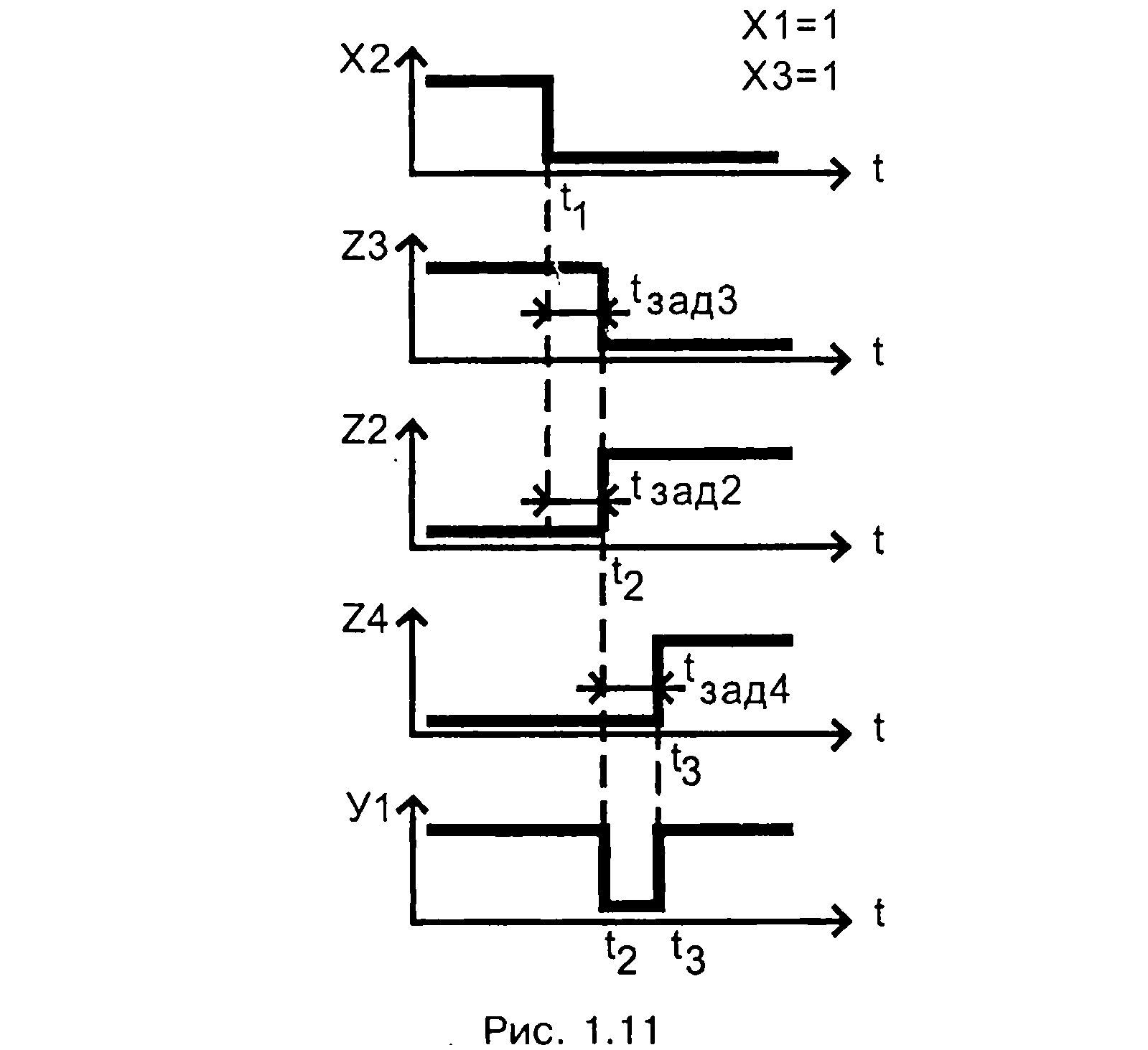
Переходные процессы связаны с конечностью скорос­ти электромагнитных процессов, протекающих в элект­ронных цепях. Входные сигналы, проходя через комбина­ционную схему, испытывают временную задержку. Мак­симальная длительность задержки (длительность переход­ных процессов) определяется числом последовательных включенных ЛЭ. Временные задержки в комбинационных схемах могут привести к кратковременным сбоям, лож­ным срабатываниям. Рассмотрим пример (рис. 1.10)

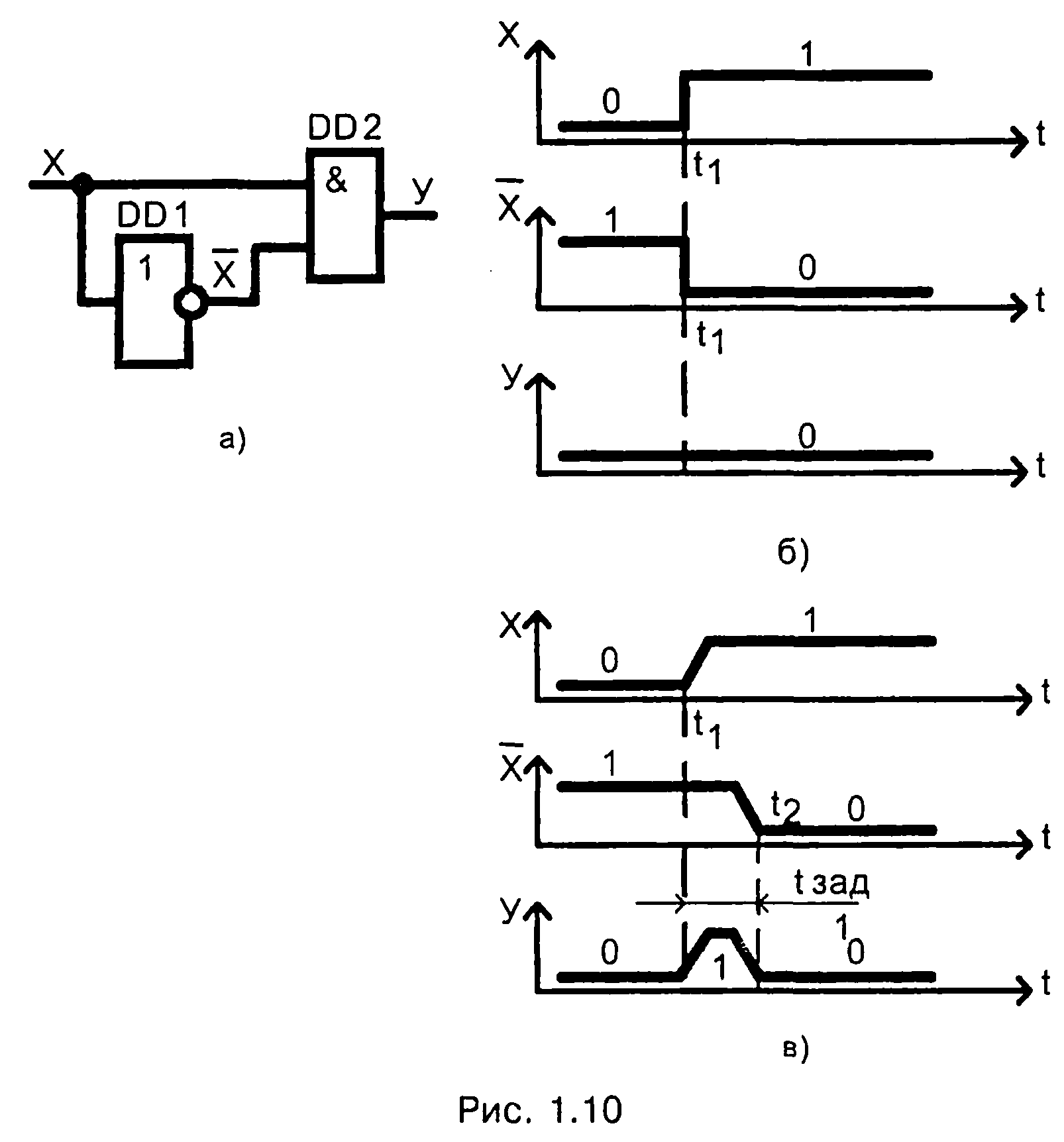
Схема на рис. 1.10, а соответствует логическому выра­жению (1.16) соотношения с нулем

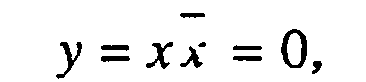
согласно которому на выходе должен быть постоянно логический ноль. Такой выходной сигнал будет при иде­альных ЛЭ (рис. 1.10, б), у которых отсутствует времен­ная задержка. Задержка распространения в элементе НЕ (DD1), равная t_3aдl = t₂ – t₁ приводит к возникновению кратковременного импульса логической единицы (рис. 1.10, в).

Анализ влияния переходных процессов на работу комбинационных устройств проводят с помощью карт Карно:

3. Единичные клетки функции объединяются в контуры.

4. Проверяется наличие соседних единичных клеток, принадлежащих различным контурам.

5. Найденные пары клеток указывают на то, что в схе­ме возможны сбои либо ложные срабатывания.

В карте Карно (таблица 1.11) для схемы рис. 1.9 вы­делим два единичных контура: контур (а) для наборов х₁х₂х₃ = (110, 111), контур (б) для наборов х₁х₂х₃= (101, 001)

Эти два контура не пересекаются и имеют две сосед­ние единичные клетки, соответствующие наборам 111-101.

Следовательно, при переходе х₁х₂х₃ = 111—> х₁х₂х₃ = 101 возможен сбой схемы (рис. 1.11).

Согласно логике работы схемы рис. 1.11 при измене­нии входной комбинации 111—>101 должна сохраняться на выходе логическая единица. Однако ввиду наличия за­держек в логических элементах НЕ (DD2) t_зад2= t₂ — t₁ ; И (DD3) t_3aд3 = t₂- t₁; И (DD4) t_зad4 = t₃ - t₂ на выходе y₁ в течение короткого интервала времени (t₃ – t₂) возникает ложный логический ноль. Это происходит из-за разности задержек распространения сигнала х₂ к выходу у₁ по мар­шрутам (DD2-DD4-DD5); (DD3-DD5).

Для исключения возможных сбоев в работе цифровых устройств используются два пути:

1. Введение дополнительных элементов, задерживаю­щих сигнал.

2. Запрещение работы схемы (либо ее части) на время переходных процессов.

Таким образом, в задаче анализа проводится учет от­личия характеристик реальных цифровых устройств от идеализированных моделей, а также определение необходимых коррекций в схеме.