СВОБОДНОЙ ПОВЕРХНОСТИ СПОСОБОМ В. ЧАРНОМСКОГО

Этот способ удобен тем, что для расчета изменения глубины вдоль открытого потока не требуется применения специальных таблиц. Способ может использоваться как для непризматических, так и для призматических русел.

Для вывода способа В. Чарномского рассмотрим неравномерный поток, представленный на рис. 8.11.

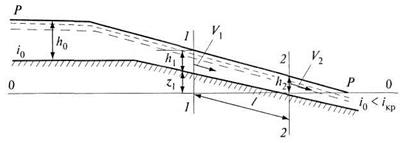
Рис. 8.11. К выводу уравнения В. Чарномского

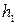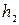Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно горизонтальной плоскости сравнения, проходящей на уровне наинизшей точки сечения 2-2. В сечении 1-1 глубина потока и скорость , а в сечении 2-2 соответственно и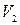

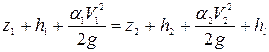. (8.33)

При уклоне дна 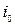понижение отметки дна русла на участке 1-1 и 2-2 длиной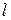

.

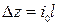Величины , ;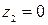

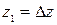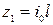. (8.34)

Гидравлические потери по длине 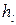на выбранном участке выразим через гидравлический уклон :

.

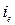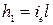Уравнение (8.33) примет следующий вид после соответствующих подстановок:

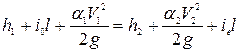. (8.35)

Удельная энергия потока в сечении 1-1

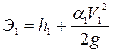. (8.36)

В сечении 2-2

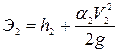. (8.37)

Тогда согласно (8.35) получим

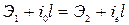. (8.38)

Разность удельных энергий в сечениях потока

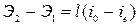. (8.39)

Считаем с некоторой степенью приближения, что гидравлические потери по длине при неравномерном движении соответствуют потерям для равномерного движения. Следовательно, гидравлический уклон можно определить по формуле Шези:

.

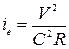Однако при определении 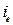принимаем его среднее значение относительно сечений 1-1 и 2-2.

Средняя скорость потока между этими сечениями

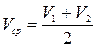. (8.40)

Среднее значение коэффициента Шези

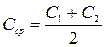. (8.41)

Средний гидравлический радиус

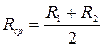. (8.42)

Средний гидравлический уклон

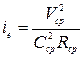. (8.43)

Окончательно получим следующее выражение для длины между выбранными сечениями:

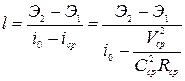. (8.44)

В связи с осреднением гидравлического уклона и заменой дифференциального уравнения уравнением в конечных разностях расстояние между сечениями по уравнению (8.44) получается достаточно приближенным. Для получения большей точности при расчете кривой свободной поверхности следует расстояние поделить на несколько большее количество участков. Чем меньше принимается расстояние между участками, тем выше получается точность расчетов.

Порядок расчетов следующий:

· устанавливается форма кривой свободной поверхности потока;

· назначается исходное сечение: например, для кривой спада - сечение с критической глубиной; для кривой подпора - сечение с нормальной глубиной;

· кривая свободной поверхности разбивается на n участков;

· определяются удельные энергии сечений в начале и конце каждого участка;

· определяются гидравлические уклоны в начале и конце каждого участка, а также среднее значение гидравлического уклона на всей длине участка;

· производится расчет длины каждого участка.

Способ, предложенный В. Чарномским, может быть применен для русла любого поперечного сечения. В случае призматического русла решение уравнения (8.44) по определению глубины в нем существенно упрощается.

Известны другие методы интегрирования дифференциального уравнения неравномерного движения - способы Н. Павловского, К. Михайлова, В. Даденкова и др.