Пример 8.3
В канале трапецеидального сечения образовался гидравлический прыжок. Глубина в начале прыжка 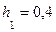 м. Требуется определить сопряженную с ней глубину прыжка
м. Требуется определить сопряженную с ней глубину прыжка 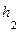 при следующих данных:
при следующих данных: 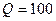 м3/с;
м3/с;  м;
м; 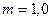 .
.
Используем условие прыжковой функции 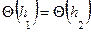 . Площадь сечения
. Площадь сечения 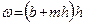 , расстояние центра тяжести сечения ус относительно свободной поверхности в канале
, расстояние центра тяжести сечения ус относительно свободной поверхности в канале
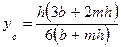 .
.
Прыжковую функцию можно представить в виде
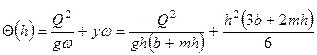 .
.
Подставив в это выражение численные значения Q, b, m, окончательно получим
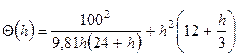 .
.
Используя последнее выражение, задаваясь разными значениями h, вычисляем прыжковую функцию. Результаты вычислений сводим в табл. 8.4.
Таблица 8.4 - Вычисление прыжковой функции
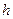 , м , м
| 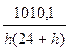
| 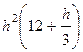
| 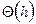 , м3 , м3
|
| 0,3 | 132,82 | 1,09 | 140,9 |
| 0,5 | 83,21 | 3,04 | 86,2 |
| 0,8 | 51,37 | 7,85 | 59,2 |
| 1,0 | 40,77 | 12,33 | 53,1 |
| 1,3 | 26,64 | 28,13 | 54,8 |
| 2,0 | 19,60 | 50,64 | 70,2 |
| 2,5 | 53,23 | 80,19 | 95,4 |
| 3,0 | 12,58 | 117,00 | 129,6 |
| 3,5 | 11,67 | 161,33 | 173,2 |
По данным табл. 8.4 построим график функции 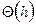 (рис. 8.15).
(рис. 8.15).
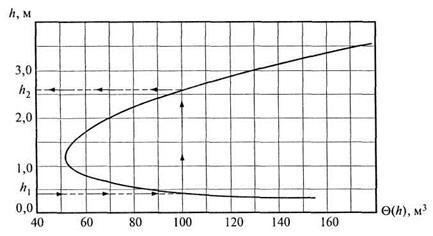
Рис. 8.15. График прыжковой функции к примеру 8.3
Зная первую глубину 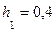 м, по графику находим сопряженную с ней глубину
м, по графику находим сопряженную с ней глубину 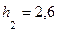 м. Этим глубинам соответствует функция
м. Этим глубинам соответствует функция 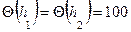 м3.
м3.
Дата добавления: 2015-09-29; просмотров: 578;
