УСТАНОВИВШЕГОСЯ МЕДЛЕННО ИЗМЕНЯЮЩЕГОСЯ ДВИЖЕНИЯ ВОДЫ В ОТКРЫТОМ РУСЛЕ
Рассмотрим установившееся неравномерное движение в открытом русле призматической формы.
Для вывода уравнения неравномерного движения принимаются следующие допущения:
· движение потока считаем установившимся, если скорость медленно изменяется по его длине;
· уклон дна 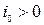 , распределение давления по поперечному живому сечению подчиняется гидростатическому закону;
, распределение давления по поперечному живому сечению подчиняется гидростатическому закону;
· распределение скорости по живому сечению неизменно, поэтому величина коэффициента Кориолиса постоянная;
· коэффициент шероховатости по длине потока постоянный.
На рис. 8.3 изображена схема неравномерного движения потока воды в призматическом русле при уклоне дна 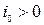 .
.
Рассмотрим два контрольных сечения 1-1 и 2-2, находящихся на бесконечно малом расстоянии друг от друга, и наметим плоскость сравнения 0-0 (рис. 8.3).
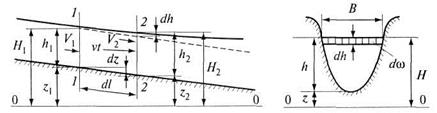
Рис. 8.3. Схема неравномерного движения жидкости в русле
Напишем уравнение Бернулли для выбранных сечений:
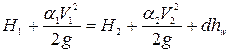 , (8.1)
, (8.1)
где 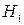 и
и 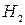 - расстояния от плоскости сравнения 0-0 до поверхности воды в сечениях 1-1 и 2-2;
- расстояния от плоскости сравнения 0-0 до поверхности воды в сечениях 1-1 и 2-2; 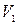 и
и 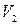 - средние скорости в сечениях;
- средние скорости в сечениях; 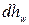 - гидравлические потери на участке длиной dl;
- гидравлические потери на участке длиной dl;
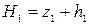 ;
; 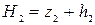 .
.
В сечении 2-2:
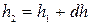 и
и 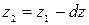 .
.
В первом сечении средняя скорость 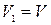 ; во втором сечении
; во втором сечении 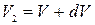 .
.
После подстановок h, z и 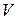 в уравнение (8.1) получим
в уравнение (8.1) получим
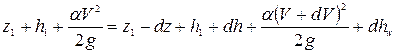 , (8.2)
, (8.2)
где 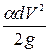 - бесконечно малая величина второго порядка, которой можно пренебречь.
- бесконечно малая величина второго порядка, которой можно пренебречь.
Преобразуем выражение (8.2):
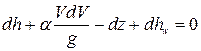 , (8.3)
, (8.3)
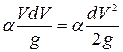 .
.
Уравнение (8.3) выразим в следующем виде:
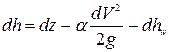 . (8.4)
. (8.4)
Разделим полученное выражение (8.4.) на длину dl:
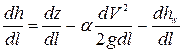 , (8.5)
, (8.5)
где 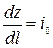 - уклон дна русла;
- уклон дна русла; 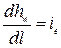 - гидравлический уклон.
- гидравлический уклон.
Выразим скоростной напор через расход:
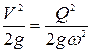 , (8.6)
, (8.6)
где 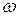 - площадь живого сечения русла,
- площадь живого сечения русла, 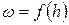 .
.
Так как 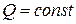 , запишем
, запишем
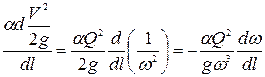 . (8.7)
. (8.7)
Площадь элементарного сечения 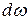 (см. рис. 8.3.)
(см. рис. 8.3.)
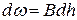 , (8.8)
, (8.8)
где 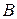 - ширина сечения по верху русла;
- ширина сечения по верху русла; 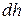 - приращение глубины потока на длине
- приращение глубины потока на длине 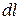 .
.
Подставим 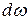 в (8.7):
в (8.7):
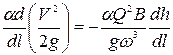 . (8.9)
. (8.9)
Гидравлические потери на участке при установившемся неравномерном движении с некоторыми допущениями возможно определить, как для равномерного движения.
Используем формулу Шези 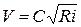 .
.
Гидравлический уклон 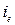
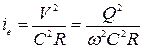 .
.
После подстановок (8.9) и 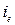 в уравнение (8.5) получим
в уравнение (8.5) получим
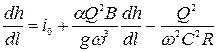 . (8.10)
. (8.10)
Выделим из (8.10) 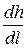 , и окончательно уравнение будет иметь следующий вид:
, и окончательно уравнение будет иметь следующий вид:
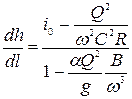 . (8.11)
. (8.11)
Полученное уравнение (8.11) называется основным дифференциальным уравнением неравномерного установившегося движения жидкости первого вида.
В уравнении (8.11) 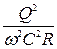 можно выразить через расходную характеристику (модуль расхода). Расходная характеристика при равномерном движении, если глубина в русле
можно выразить через расходную характеристику (модуль расхода). Расходная характеристика при равномерном движении, если глубина в русле 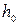 , площадь
, площадь 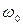 , имеет вид
, имеет вид
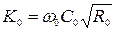 , (8.12)
, (8.12)
где 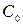 ,
, 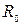 - коэффициент Шези и гидравлический радиус при равномерном движении.
- коэффициент Шези и гидравлический радиус при равномерном движении.
Для неравномерного движения расходная характеристика имеет вид
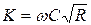 .
.
Расход через расходную характеристику составит
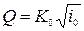 .
.
Таким образом,
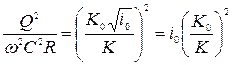 . (8.13)
. (8.13)
Дифференциальное уравнение (8.11) можно представить в виде
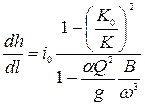 . (8.13)
. (8.13)
Дата добавления: 2015-09-29; просмотров: 1047;
