Приток воды к совершенному грунтовому колодцу при безнапорном движении фильтрационного потока
На рис. 11.4 изображена схема трубчатого колодца радиусом r0, погруженного до водоупора. Уровень грунтовых вод располагается на высоте H0 над водоупором. Глубина воды водонасыщенного слоя H0 называется мощностью водоносного пласта.
При отборе воды из колодца движение фильтрационного потока будет неравномерным. Полагаем, что стенки колодца полностью водопроницаемы.
В результате отбора воды из трубчатого колодца уровень ее в нем будет понижаться, так же как и уровень около колодца. Вокруг колодца в водоносном пласте образуется воронкообразная свободная поверхность с центром в колодце. Эта свободная поверхность является депрессионной воронкой. Кривая, ограничивающая эту воронку, - депрессионная линия.
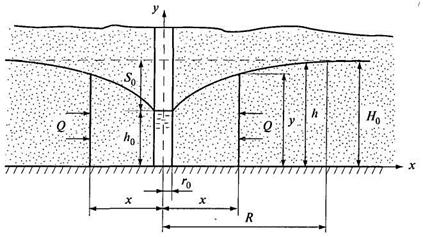
Рис. 11.4. Приток воды к совершенному трубчатому колодцу
Расстояние R, на котором депрессионная линия соединяется с начальным уровнем воды, называется радиусом депрессии (радиус влияния отдельного колодца). Влияние откачки воды из колодца за пределами радиуса депрессии не наблюдается, там уровень воды остается постоянным.
Проведем координатные оси: ось х проходит по поверхности водоупора, а ось у - по вертикальной оси колодца (см. рис. 11.4).
Выделим объем водоносного грунта вокруг колодца в виде цилиндра, высота, которого у, радиус х. Через поверхность этого цилиндра 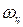 будет протекать расход Q.
будет протекать расход Q.
Расход воды, притекающей к цилиндру,
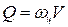 , (11.17)
, (11.17)
где 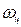 ; V - средняя скорость.
; V - средняя скорость.
В выбранном сечении будет иметь место плавно изменяющееся безнапорное движение воды. Следовательно, средняя скорость в данном сечении, согласно формуле Дюпюи 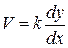 .
.
Дифференциальное уравнение притока воды к колодцу
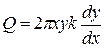 . (11.18)
. (11.18)
Разделим переменные в выражении (11.18):
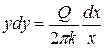 . (11.19)
. (11.19)
Уравнение (11.19) интегрируем согласно граничным условиям - значения х изменяются от r0 до R, а у - от h0 до H0:
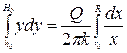 ;
; 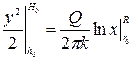 .
.
Окончательно получим
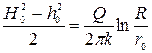 . (11.20)
. (11.20)
Отсюда приток к совершенному колодцу (дебит его) после преобразований (11.20)
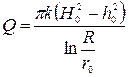 . (11.21)
. (11.21)
Используя понятие понижения уровня воды в колодце S0=H0 - h0, приток воды к колодцу
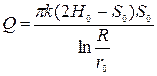 . (11.22)
. (11.22)
Уравнение кривой депрессии можно получить из уравнения (11.20), приняв изменения линейных параметров от r0 до х и от h0 до у:
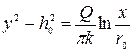 (11.23)
(11.23)
где х и у - координаты кривой депрессии.
Глубина воды на расстоянии х равна у=h, тогда уравнение кривой депрессии будет иметь следующий вид:
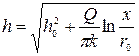 . (11.24)
. (11.24)
Радиус влияния колодца R может быть вычислен по формуле В. Зихарда, м,
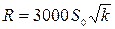 , (11.25)
, (11.25)
где S0, h - в метрах, k - в метрах в секунду.
В табл. 11.2 приведены ориентировочные значения радиуса влияния (депрессии) для песчаных грунтов в неограниченном пласте грунта.
Таблица 11.2 - Значения радиуса влияния песчаных грунтов
| Грунт | R, м |
| Мелкозернистый песок | 100-200 |
| Среднезернистый песок | 250-500 |
| Крупнозернистый песок | 700-1000 |
Наиболее достоверные данные о значении радиуса влияния R можно получить только в результате гидрогеологических изысканий.
Дата добавления: 2015-09-29; просмотров: 2406;
