ЗАКОН ФИЛЬТРАЦИИ
Н. Дарси в 1895 г. были произведены многочисленные опыты с различными песчаными грунтами, помещенными в цилиндрическую трубу.
Опыты производились в условиях установившейся фильтрации воды через песчаный грунт. К стенке трубы на расстоянии l были присоединены пьезометры. В опытах гидравлические потери напора hw определялись по разности уровней воды Н1 и Н2 в пьезометрах:
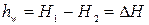 . (11.4)
. (11.4)
В результате проведенных экспериментов Н. Дарси было установлено, что имеет место линейная зависимость между фильтрационным расходом в трубе с песчаными грунтами и гидравлическими потерями.
На основании опытов Дарси была получена следующая экспериментальная зависимость:
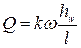 , (11.5)
, (11.5)
где 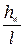 - гидравлический уклон, обозначаемый через
- гидравлический уклон, обозначаемый через  ;
; 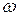 - площадь сечения трубы; k - коэффициент, характеризующий водопроницаемость песчаного грунта.
- площадь сечения трубы; k - коэффициент, характеризующий водопроницаемость песчаного грунта.
Средняя скорость фильтрационного потока
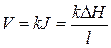 . (11.6)
. (11.6)
Линейная зависимость (11.6) является законом фильтрации Дарси. Коэффициент k получил название коэффициента фильтрации, он имеет размерность скорости и является постоянным для данного песка или другого пористого материала.
При рассмотрении фильтрации в какой-нибудь области пористой среды (рыхлые породы грунта) следует иметь в виду, что скорость фильтрации существенно мала, поэтому величиной скоростного напора можно пренебречь. Полный напор в этом случае будет представлять собой гидростатический напор. Гидравлические потери на участке фильтрационного потока - разность гидростатических напоров на участках.
Гидравлический уклон в данном случае будет равен пьезометрическому уклону. В связи с тем, что гидравлические потери линейны скорости фильтрации, можно считать, что движение жидкости в области фильтрации является ламинарным.
Выделим струйку жидкости в области фильтрации при напорном движении (см. рис. 11.1). На участке длиной ∆l гидравлические потери равны ∆hw, т.е. разности пьезометрических напоров ∆Н, а уклон на участке 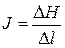 .
.
На участке длиной dl уклон убывает и равен
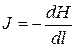 . (11.7)
. (11.7)
При линейном отношении между скоростью u и 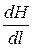 скорость в точке а
скорость в точке а
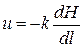 . (11.8)
. (11.8)
Данная формула, выражающая скорость u в точке, представляет собой закон фильтрации Дарси в дифференциальной форме.
Исследованиями, проведенными отечественными учеными, по выявлению режима движения жидкости в пористой среде было установлено, что в некоторых случаях имеет место отклонение от линейной зависимости гидравлических потерь и скорости фильтрации. Закон Дарси, как показали эксперименты, справедлив при условии, когда число Рейнольдса при фильтрации
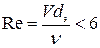 , (11.9)
, (11.9)
где dэ - эффективный диаметр частиц рыхлого материала; v - кинематическая вязкость фильтрующей жидкости.
Закон Дарси нарушается в случае, если Re>6.
Эффективный диаметр твердой частицы материала может быть вычислен по формуле
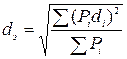 , (11.10)
, (11.10)
где di и Рi принимают по кривой гранулометрического состава грунта (материала); Рi - процентное содержание в объеме грунта частиц крупностью di.
В некоторых случаях dэ принимается равным средней крупности твердых частиц dср, dэ= dср.
Как показали опыты, при фильтрации воды в крупнозернистых, гравелистых песках и трещиноватых горных породах имеет место нелинейная фильтрация, и в этом случае наиболее подходит следующая двухчленная формула:
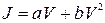 , (11.11)
, (11.11)
где a, b - некоторые постоянные коэффициенты.
Значения а и b определяются экспериментально.
При малых скоростях можно пренебречь величиной bV2 и формула (11.11) приобретет вид закона Дарси.
Коэффициент фильтрации является важнейшей величиной в фильтрационных расчетах.
Коэффициент фильтрации k определяется следующими способами:
• с помощью эмпирических формул, в которые входят физико-механические свойства фильтрующего материала;
• лабораторным методом с использованием специальных фильтрационных приборов;
• методом пробных откачек из массива грунта в условиях естественного его залегания.
Для вычисления коэффициента фильтрации k с помощью эмпирических формул необходимо знать гранулометрический состав грунта, который характеризуется кривой неоднородности (см. рис. 10.2). Известны формулы для определения k, полученные разными авторами.
Для примера приведем эмпирическую формулу И. Зауербрея, см/с,
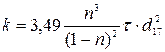 , (11.12)
, (11.12)
где n - пористость грунта; d17 - диаметр частиц грунта, масса которых вместе с более мелкими по размеру частицами составляет 17% массы всего грунта; 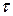 - коэффициент, учитывающий вязкость воды в зависимости от ее температуры t° (С°),
- коэффициент, учитывающий вязкость воды в зависимости от ее температуры t° (С°), 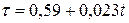 .
.
Как правило, вычисленные значения k служат для первоначальной оценки фильтрации и сравнения с другими способами определения коэффициента.
Лабораторный способ заключается в том, что используется фильтрационный прибор, который представляет собой цилиндр с сеткой в нижней его части. Грунт в виде цилиндрического образца (керна), желательно без нарушения его естественного состояния, помещается в прибор.
На стенке цилиндра имеются несколько отверстий, находящихся на расстоянии l друг от друга, к которым присоединены пьезометры (рис. 11.2).
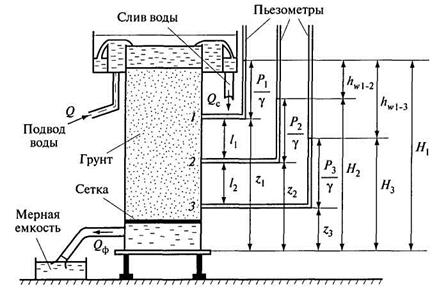
Рис. 11.2. Фильтрационный прибор
В верхней части прибора поддерживается постоянный уровень. Часть подаваемого в фильтрационный прибор расхода воды (Qc) сливается через водослив, а другая часть (Qф) фильтруется через грунт, находящийся в цилиндре. Фильтрационный расход Qф определяется объемным способом.
Гидравлические потери напора при фильтрации воды находятся по разности показаний пьезометров:
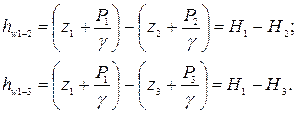 ; (11.13)
; (11.13)
 Зная площадь цилиндра
Зная площадь цилиндра 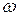 и расстояние l между отверстиями присоединения пьезометров и фильтрационный расход, вычисляется коэффициент фильтрации
и расстояние l между отверстиями присоединения пьезометров и фильтрационный расход, вычисляется коэффициент фильтрации
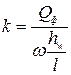 . (11.14)
. (11.14)
Метод пробных откачек используется при гидрогеологических исследованиях. На определенном расстоянии в массиве пласта фунта устраиваются несколько буровых скважин. Заглубление скважин должно быть ниже уровня воды в фильтрационном пласте грунта. Определяя расход воды из скважины и зная уровни воды в скважинах, вычисляется коэффициент фильтрации по формулам, приведенным в справочниках [7, 8]. Данный способ является достаточно достоверным, так как массив грунта находится в естественном, ненарушенном состоянии.
Фильтрационные свойства различных материалов, используемых в дренажных и водозаборных сооружениях, приведены в справочниках, например в справочнике А. Курганова и Н. Федорова [5].
Некоторые значения коэффициента фильтрации для грунтов приведены в табл. 11.1.
Таблица 11.1 - Ориентировочные значения коэффициентов фильтрации для грунтов
| Грунт | k×10 -5, м/с |
| Песок гравелистый | 100-200 |
| Крупнозернистый песок | 10-50 |
| Среднезернистый песок | 1-5 |
| Песок мелкозернистый | 0,5-2 |
| Песок глинистый | 0,1-1 |
| Супесь плотная | 0,1-0,5 |
| Суглинок | Менее 0,1 |
| Глина | Менее 0,1 |
Дата добавления: 2015-09-29; просмотров: 1740;
