Описание метода измерения. Перед началом работы необходимо ознакомиться с основными определениями, изложенными в работах 1 и 2 (интерференция света

Перед началом работы необходимо ознакомиться с основными определениями, изложенными в работах 1 и 2 (интерференция света, оптическая разность хода, показатель преломления).

Показатель преломления n является практически важной величиной, поскольку от него зависят характер распространения световой волны в веществе. Показатель преломления плоскопараллельной пластины можно измерить, используя законы геометрической оптики, в частности, закон преломления Снеллиуса:

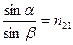(1)

где a - угол падения светового луча на границу двух сред, b - угол преломления, n₂₁ = n₂ /n₁ – относительный показатель преломления двух сред, n₁, n₂ - абсолютные показатели преломления.

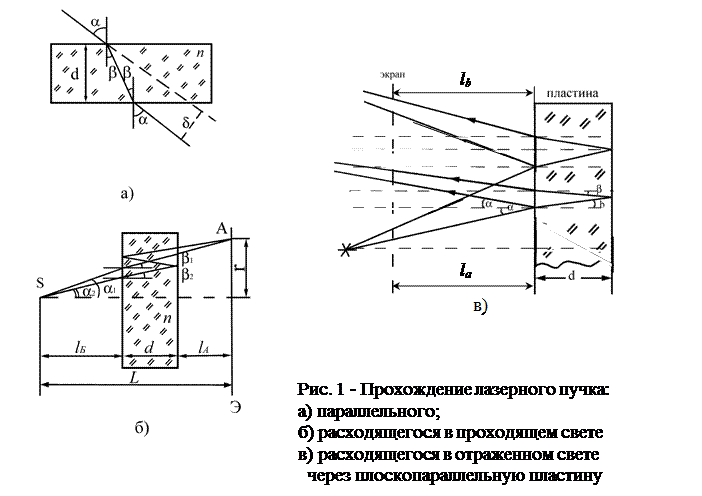
Пусть световой луч падает на пластину толщины d под углом a (рис.1). В этом случае n₁ = 1 (воздух), n₂ = n (стекло). Из пластины луч выйдет под тем же углом, но смещенным на некоторое расстояние d. Измерив расстояние d, толщину пластины d и угол a, можно определить показатель преломления п. Однако точность этого метода невысока, особенно, если пластина имеет малую толщину, поскольку на практике приходится иметь дело не с лучами, а со световыми пучками конечной толщины.

В настоящей работе рассматривается другой, интерференционный метод определения показателя преломления, который не имеет принципиальных ограничений, связанных с толщиной пластины. Если осветить плоскопараллельную пластину осесимметричной расходящейся световой волной, то на экране, установленном после пластины, будет наблюдаться интерференционная картина в виде чередующихся темных и светлых колец.

Эта картина возникает в результате наложения света, прошедшего через пластину, и света, дважды отраженного от поверхности пластины. Такие кольца являются примером полос равного наклона. Аналогичная картина будет наблюдаться и в отраженном свете, но там, где в проходящем свете наблюдались темные полосы, в отраженном будут светлые и наоборот. Это происходит потому, что в случае отраженного света одна из интерферирующих волн отражается от оптически более плотной среды, что приводит к изменению фазы этой волны на противоположную, а это эквивалентно увеличению оптической разности хода на l/2.

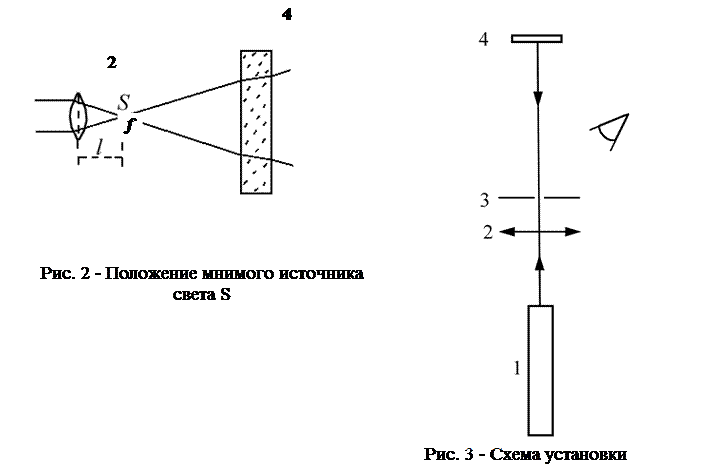
Путь двух лучей из расходящегося пучка, приходящих в одну точку на экране, показан на рис.1б. Если оптическая разность хода этих двух лучей составляет целое число длин волн тl, то в точке А будет наблюдаться максимум освещенности. Если же оптическая разность хода составляет полуцелое число длин волн (2т + 1) l/2, то в точке А будет наблюдаться минимум. Расходящийся световой пучок можно получить из параллельного пучка с помощью линзы (рис.2). Если фокусное расстояние линзы f много больше поперечных размеров исходного параллельного пучка, то угол расходимости q получается малым. В этом случае все углы a можно считать малыми, т.е. 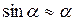, а 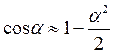. Фокус линзы можно рассматривать как точечный источник света S, из которого выходит расходящийся пучок лучей. Оптическая разность хода лучей , изображенных на рис.2., определяется следующим соотношением:

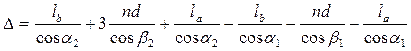(2)

Полное расстояние от фокуса линзы до экрана

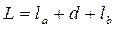(3)

Если расстояние L неограниченно увеличивать, то разность между величинами углов a₁ и a₂ будет стремиться к нулю. Поэтому в случае L>>d углы a₁ и a₂ можно заменить одним углом a (соответственно b₁ и b₁ углом b). Тогда оптическая разность хода D будет определяться следующим соотношением:

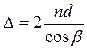(4)

Учитывая малость угла b, а также то, что 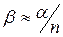(согласно закону Снеллиуса) и 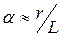, выражение (4) можно переписать следующим образом:

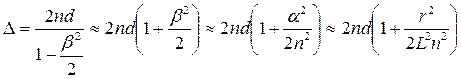(5)

Используя условие максимума D=тl, получим выражение для радиуса т-го светлого кольца:

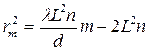(6)

Отсюда следует, что зависимость 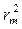от т линейная. Наклон этой прямой определяется выражением

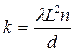(7)

Если известны длина световой волны l, расстояние L и толщина пластины d, то можно определить показатель преломления материала, из которого изготовлена пластина:

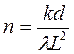(8)

Следует отметить, что для нахождения L (смотри по схеме ход луча) более удобно измерить расстояние, которое проходит световой пучок от линзы до экрана, а затем вычесть из него фокусное расстояние, если линза собирающая, или прибавить, если линза рассеивающая. Такой прием оправдан, если используемая линза является тонкой, т.е. ее толщина много меньше обоих радиусов кривизны.