Пирамида. Усеченная пирамида
Пирамидой называется многогранник, одна из граней которого – многоугольник (основание), а все остальные грани – треугольники с общей вершиной (боковые грани) (рис. 12.15). Пирамида называется правильной, если ее основанием является правильный многоугольник и вершина пирамиды проектируется в центр основания (рис. 12.16). Треугольная пирамида, у которой все ребра равны, называется тетраэдром.
 |  |
Рис. 12.15 Рис. 12.16
Боковым ребром пирамиды называется сторона боковой грани, не принадлежащая основанию. Высотой пирамиды называется расстояние от ее вершины до плоскости основания. Все боковые ребра правильной пирамиды равны между собой, все боковые грани – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из вершины, называется апофемой. Диагональным сечением называется сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Площадью боковой поверхности пирамиды называется сумма площадей всех боковых граней. Площадью полной поверхности называется сумма площадей всех боковых граней и основания.
Теоремы:
1. Если в пирамиде все боковые ребра равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности, описанной около основания.
2. Если в пирамиде все боковые ребра имеют равные длины, то вершина пирамиды проектируется в центр окружности, описанной около основания.
3. Если в пирамиде все грани равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности, вписанной в основание.
Для вычисления объема произвольной пирамиды верна формула:
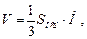
где V – объем; Sосн – площадь основания; H – высота пирамиды.
Для правильной пирамиды верны формулы:
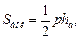
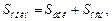
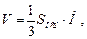
где Sбок – площадь боковой поверхности; p – периметр основания; hа – апофема; Sполн – площадь полной поверхности; Sосн – площадь основания; V – объем правильной пирамиды; H – высота.
Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды (рис. 12.17). Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды.
Основания усеченной пирамиды – подобные многоугольники. Боковые грани – трапеции. Высотой усеченной пирамиды называется расстояние между ее основаниями. Диагональю усеченной пирамиды называется отрезок, соединяющий ее вершины, не лежащие в одной грани. Диагональным сечением называется сечение усеченной пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

Рис. 12.17
Для усеченной пирамиды справедливы формулы:
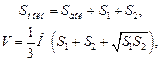 (12.4)
(12.4)
где Sполн – площадь полной поверхности; Sбок – площадь боковой поверхности; S1, S2 – площади верхнего и нижнего оснований; V – объем усеченной пирамиды; H – высота.
Для правильной усеченной пирамиды верна формула:
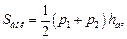
где p1 , p2 – периметры оснований; hа – апофема правильной усеченной пирамиды.
Пример 1. В правильной треугольной пирамиде двугранный угол при основании равен 60º. Найти тангенс угла наклона бокового ребра к плоскости основания.
Решение. Сделаем рисунок (рис. 12.18).
Рис. 12.18
Пирамида правильная, значит в основании лежит равносторонний треугольник и все боковые грани – равные равнобедренные треугольники. Двугранный угол при основании – это угол наклона боковой грани пирамиды к плоскости основания. Линейным углом будет угол a между двумя перпендикулярами: 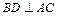 и
и 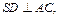 т. е.
т. е. 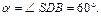 Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС). Угол наклона бокового ребра (например SB) – это угол между самим ребром и его проекцией на плоскость основания. Для ребра SB этим углом будет угол SBD. Чтобы найти тангенс
Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС). Угол наклона бокового ребра (например SB) – это угол между самим ребром и его проекцией на плоскость основания. Для ребра SB этим углом будет угол SBD. Чтобы найти тангенс 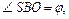 необходимо знать катеты SO и OB. Пусть длина отрезка BD равна 3а. Точкой О отрезок BD делится на части:
необходимо знать катеты SO и OB. Пусть длина отрезка BD равна 3а. Точкой О отрезок BD делится на части: 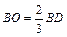 и
и 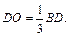 Из
Из 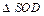 находим SO:
находим SO:
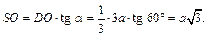
Из 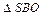 находим:
находим: 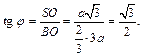
Получаем ответ: 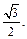
Пример 2. Найти объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны 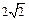 см и
см и 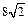 см, а высота – 4 см.
см, а высота – 4 см.
Решение. Для нахождения объема усеченной пирамиды воспользуемся формулой (12.4). Чтобы найти площади оснований, необходимо найти стороны квадратов-оснований, зная их диагонали. Стороны оснований равны соответственно 2 см и 8 см. Значит, площади оснований равны 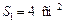 и
и 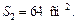 Подставив все данные в формулу, вычислим объем усеченной пирамиды:
Подставив все данные в формулу, вычислим объем усеченной пирамиды:
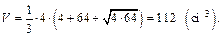
Получаем ответ: 112 см3.
Пример 3. Найти площадь боковой грани правильной треугольной усеченной пирамиды, стороны оснований которой равны 10 см и 4 см, а высота пирамиды – 2 см.
Решение. Сделаем рисунок (рис. 12.19).

Рис. 12.19
Боковой гранью данной пирамиды является равнобокая трапеция. Для вычисления площади трапеции необходимо знать основания и высоту. Основания даны по условию, остается неизвестной только высота. Ее найдем из 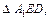 где А1Е – перпендикуляр из точки А1 на плоскость нижнего основания, A1D – перпендикуляр из точки А1 на АС. А1Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 12.20). Точка О – проекция центров верхнего и нижнего оснований.
где А1Е – перпендикуляр из точки А1 на плоскость нижнего основания, A1D – перпендикуляр из точки А1 на АС. А1Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 12.20). Точка О – проекция центров верхнего и нижнего оснований. 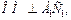
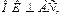
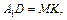 так как
так как 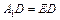 (рис. 12.20) и
(рис. 12.20) и 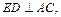
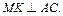 С другой стороны, ОК – радиус вписанной в
С другой стороны, ОК – радиус вписанной в 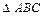 окружности и
окружности и 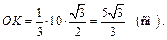 ОМ – радиус вписанной в
ОМ – радиус вписанной в 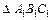 окружности:
окружности:
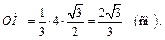
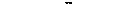
Рис. 12.20
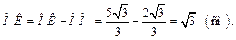 MK = DE.
MK = DE.
По теореме Пифагора из 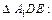
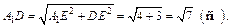
Площадь боковой грани: 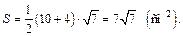
Получаем ответ: 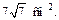
Пример 4. В основании пирамиды лежит равнобокая трапеция, основания которой а и b (a > b). Каждая боковая грань образует с плоскостью основания пирамиды угол, равный j. Найти площадь полной поверхности пирамиды.
Решение. Сделаем рисунок (рис. 12.21).

Рис. 12.21
Площадь полной поверхности пирамиды SABCD равна сумме площадей 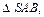
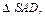
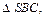
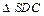 и площади трапеции ABCD.
и площади трапеции ABCD.
Воспользуемся утверждением, что если все грани пирамиды равнонаклонены к плоскости основания, то вершина проектируется в центр вписанной в основание окружности. Точка О – проекция вершины S на основание пирамиды. Треугольник SOD является ортогональной проекцией треугольника CSD на плоскость основания. По теореме о площади ортогональной проекции плоской фигуры имеем:
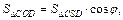 откуда получаем:
откуда получаем: 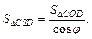
Аналогично 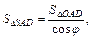
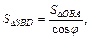
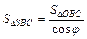 и, значит,
и, значит, 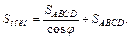 Таким образом, задача свелась к нахождению площади трапеции АВСD. Изобразим трапецию ABCD отдельно (рис. 12.22). Точка О – центр вписанной в трапецию окружности.
Таким образом, задача свелась к нахождению площади трапеции АВСD. Изобразим трапецию ABCD отдельно (рис. 12.22). Точка О – центр вписанной в трапецию окружности.

Рис. 12.22
Так как в трапецию можно вписать окружность, то 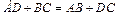 или
или 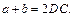 Из
Из 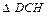 по теореме Пифагора имеем:
по теореме Пифагора имеем:
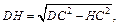
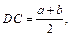
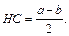
Тогда 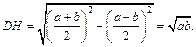
Площадь трапеции: 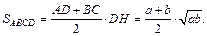
Следовательно,
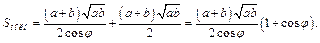
Получаем ответ: 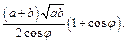
Пример 5.Основание пирамиды – равносторонний треугольник со стороной а. Одна из боковых граней – равнобедренный прямоугольный треугольник, плоскость которого перпендикулярна плоскости основания. Найти площадь боковой поверхности пирамиды.
Решение. Сделаем рисунок (рис. 12.23).

Рис. 12.23
Площадь боковой поверхности данной пирамиды SABC состоит из суммы площадей ее боковых граней. Боковые грани – треугольники, один из которых прямоугольный и равнобедренный ( 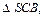
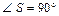 ), два других – равные треугольники
), два других – равные треугольники 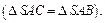 Рассмотрим
Рассмотрим 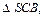
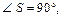
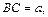
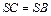 – по условию. Вычислим его площадь:
– по условию. Вычислим его площадь: 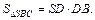 Так как
Так как 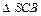 равнобедренный, то
равнобедренный, то 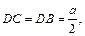 а так как
а так как 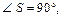 то
то 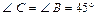 и, следовательно, в
и, следовательно, в 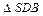
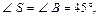
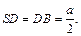
Тогда 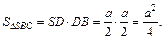
Рассмотрим 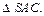
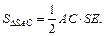 SE найдем из
SE найдем из 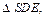
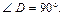 По теореме Пифагора имеем
По теореме Пифагора имеем 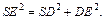 Найдем DE. Для этого рассмотрим равносторонний треугольник основания (рис. 12.24).
Найдем DE. Для этого рассмотрим равносторонний треугольник основания (рис. 12.24). 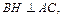
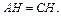
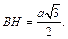 В
В 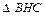 отрезок DE является средней линией, следовательно,
отрезок DE является средней линией, следовательно, 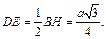 Находим SE:
Находим SE:
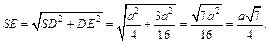

Рис. 12.24
Теперь 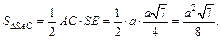
Площадь боковой поверхности пирамиды равна:
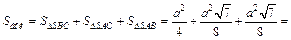
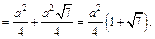
Получаем ответ: 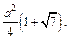
Дата добавления: 2015-09-29; просмотров: 2648;
