Инерциальное звено второго порядка. Колебательное звено.

Дифференциальное уравнение инерционного звена второго порядка:

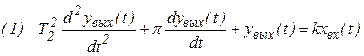
в операторной форме:

Т²₂p²y_вых(p) + T₁py_вых(p) + y_вых(p) = kx_вх(p)

Передаточная функция:

Переходную характеристику звена можно найти классическим способом, решая дифференциальное уравнение звена, когда в правой части 1(t)=x_вх(t)

Решение однородного уравнения определяются корнями характеристического уравнения звена, которое имеет вид:

Т²₂p² + T₁p + 1 = 0

Возможно два случая:

1) Т₁³2Т₂ (Т₁/2Т₂ = d ³ 1); p_1,2 = - a_1,2

В этом случае полное решение уравнения, т.е. переходная характеристика, может быть записана следующим образом:

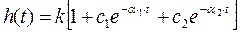
где С₁, С₂ – постоянные интегрирования, определяемые из начальных условий. Характеристика звена в этом случае имеет вид:

Звено в этом случае называется инерционным второго порядка.

2) T₁ < 2T₂ (T₁/2T₂ = d < 1) p_1,2 = - a ± jb .

В этом случае в общем виде переходную характеристику можно записать как:

h(t) = k [1 + Ae^–at sin(bt + j)],

где А и определяются из начальных условий.

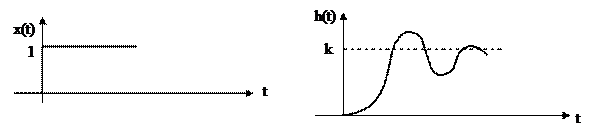
Переходная характеристика в этом случае представляется затухающими колебаниями, и звено в этом случае называется колебательным звеном. Переходные характеристики звена второго порядка можно определить также в операторной форме из передаточной функции, а оригинал найти из таблиц преобразования Лапласа.

Уравнение звена второго порядка для случая T₁/2T₂<1 переписывается через параметры колебательного звена в виде:

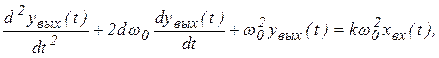
где w₀ - частота собственных колебаний звена; d-коэффициент затухания. Параметры колебательного звена связаны с параметрами инерционного звена второго порядка соотношениями:

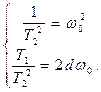
Частотные характеристики звена определяются из комплексной передаточной функции:

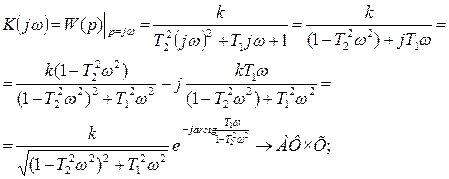
ФЧХ: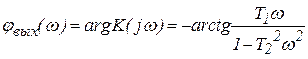

Тема 3

Структурные схемы САР. Правила структурных преобразований

При математическом описании САР обычно изображают в виде блок-схемы и для каждого “блока” (элемента) записывают уравнения, исходя из физических законов, которым подчиняются процессы в нём. Структурную схему можно составить на основании этой блок-схемы и полученных уравнений (передаточных функций). И дальнейшие преобразования, необходимые для получения уравнений и передаточных функций системы, проще и нагляднее производить по структурной схеме.