Теорема о существовании МЦУ

Пусть ускорение полюса, например точки А, равно 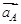(рис. 34).

Тогда, если 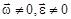, то МЦУ существует

Отложим отрезок AQ под углом a в направлении e (рис. 34).

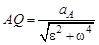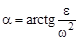; . (47)

Найдем ускорение точки Q :

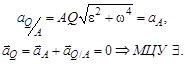
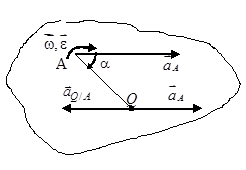
Рис. 34

Таким образом, МЦУ принадлежит отрезку, расположенному под углом 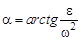к вектору ускорения 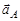, который откладывается от ускорения полюса в сторону, соответствующую «направлению вращения» 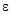, на расстояние (от полюса), равное

.

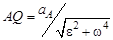На основании сказанного можно сконструировать «крестовую» формулу, аналогичную такой же формуле для скоростей точек:

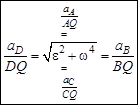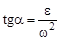; . (48)

Модули ускорения точек плоской фигуры в каждый момент времени пропорциональны расстояниям от этих точек до МЦУ, а вектор ускорений составляет с отрезками, соединяющими эти точки с МЦУ, один и тот же угол α.