Коэффициент корреляции Пирсона

Коэффициент корреляции Пирсона r, который является безразмерным индексом в интервале от -1,0 до 1,0 включительно, отражает степень линейной зависимости между двумя множествами данных.

Показатель тесноты связи между двумя признаками определяется по формуле линейного коэффициента корреляции:

где x - значение факторного признака;

y - значение результативного признака;

n - число пар данных.

Парная корреляция - это связь между двумя признаками: результативным и факторным или двумя факторными.

Варианты связи, характеризующие наличие или отсутствие линейной связи между признаками:

· большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция) - наличие прямой линейной связи;

· малые значения одного набора связаны с большими значениями другого (отрицательная корреляция) - наличие отрицательной линейной связи;

· данные двух диапазонов никак не связаны (нулевая корреляция) - отсутствие линейной связи.

В качестве примера возьмем набор данных А(таблица 8.1). Необходимо определить наличие линейной связи между признаками x и y.

Для графического представления связи двух переменных использована система координат с осями, соответствующими переменным x и y. Построенный график, называемый диаграммой рассеивания, показан на рисунке 8.2. Данная диаграмма показывает, что низкие значения переменной x соответствуют низким значениям переменной y, высокие значения переменной x соответствуют высоким значениям переменной y. Этот пример демонстрирует наличие явной связи.

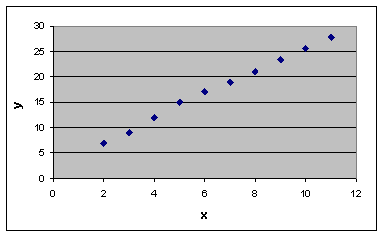
Рисунок 8.2 - Диаграмма рассеивания

Таким образом, мы можем установить зависимость между переменными x и y. Рассчитаем коэффициент корреляции Пирсона между двумя массивами (x и y) при помощи функции MS Excel ПИРСОН(массив1;массив2). В результате получаем значение коэффициент корреляции равный 0,998364, т.е. связь между переменными x и y является весьма высокой. Используя пакет анализа MS Excel и инструмент анализа "Корреляция", можем построить корреляционную матрицу.

Любая зависимость между переменными обладает двумя важными свойствами: величиной и надежностью. Чем сильнее зависимость между двумя переменными, тем больше величина зависимости и тем легче предсказать значение одной переменной по значению другой переменной. Величину зависимости легче измерить, чем надежность.

Надежность зависимости не менее важна, чем ее величина. Это свойство связано с представительностью исследуемой выборки. Надежность зависимости характеризует, насколько вероятно, что эта зависимость будет снова найдена на других данных.

С ростом величины зависимости переменных ее надежность обычно возрастает.