Линейные уравнения и граничные задачи фильтрации.
1. Модель ламинарной фильтрации ньютоновских однородных жидкостей в изотропной среде
Для этой модели справедлив экспериментально установленный линейный закон фильтрации Дарси
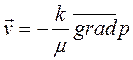 , ,
| (2.30) |
Или в проекциях на оси декартовой системы координат
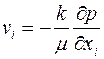 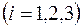 , ,
|
где 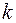 называется коэффициентом проницаемости, или просто проницаемостью.
называется коэффициентом проницаемости, или просто проницаемостью.
Проницаемость имеет размерность площади. Она не зависит от свойств жидкости, является чисто геометрической характеристикой пористой среды.
В практике принято проницаемость измерять в мкм2. Среда имеет проницаемость 1 мкм2 если при градиенте давления 10 МПа/м через площадку 10-4 м2 расход жидкости, вязкость которой 10-3 Па.с, составляет 10-6 м3/с, т. е. 1мкм2 = 10-12 м2.
Проницаемость определяется геометрией порового пространства. Известно множество попыток установить аналитическую зависимость между проницаемостью, пористостью, размером, формой и упаковкой частиц.
Для фиктивного грунта Слихтер нашел, что теоретическая проницаемость
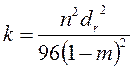 , ,
|
а Козени получил
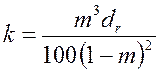 . .
|
Эти формулы полезны при изучении закономерностей фильтрации только в искусственных пористых телах. Для реальных тел достоверные результаты можно получить лишь по данным измерений расхода и перепада давления в лабораторных условиях на керновом материале или при натуральных испытаниях пластов с последующей интерпретацией полученных результатов.
Закон фильтрации (2.30) – это упрощенная форма уравнений движения
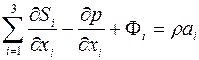 , ,
|
неразрывности движения или сохранения массы
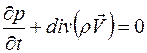 , ,
|
и механического состояния
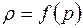 , ,
|
в которых отброшены силы инерции 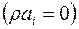 , а сумма сил
, а сумма сил 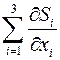 заменена силами трения Ньютона
заменена силами трения Ньютона 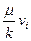 . Тогда отпадает надобность в уравнениях состояния (2.24).
. Тогда отпадает надобность в уравнениях состояния (2.24).
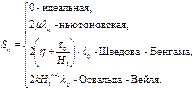
|
Имеем симметричный девиатор напряжений
Принимается, что при небольших изменениях порового давления пористость и проницаемость среды, а также плотность жидкости линейно зависят от 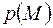 , т. е.
, т. е.
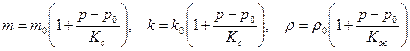
| (2.31) |
где 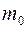 ,
, 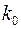 и
и 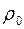 – соответственно пористость, проницаемость и плотность при начальном давлении
– соответственно пористость, проницаемость и плотность при начальном давлении 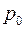 ;
; 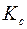 и
и 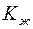 – соответственно модули объемной упругости скелета и жидкости. Кроме того, принимаем, что
– соответственно модули объемной упругости скелета и жидкости. Кроме того, принимаем, что 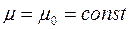 .
.
К уравнениям (2.30 и (2.31) необходимо присоединить еще уравнение неразрывности движения жидкости (2.22), которое в силу неполного, равного 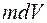 , заполнения элементарного объема
, заполнения элементарного объема 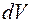 сплошной среды принимает вид
сплошной среды принимает вид
 . .
| (2.32) |
Уравнения (2.30) – (2.32) образуют, таким образом, замкнутую систему для определения функций 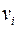 ,
, 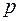 ,
, 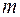 и
и 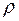 . Но если подставить уравнения (2.30) и (2.31) в (2.32) и учесть, что в реальных ситуациях величины
. Но если подставить уравнения (2.30) и (2.31) в (2.32) и учесть, что в реальных ситуациях величины 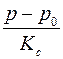 и
и  много меньше единицы, то отбросив малые величины высших порядков, получим одно основное
много меньше единицы, то отбросив малые величины высших порядков, получим одно основное
классическое уравнение теории фильтрации:
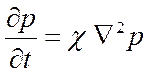 , ,
| (2.33) |
где 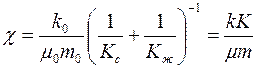 – коэффициент пьезопроводности среды;
– коэффициент пьезопроводности среды; 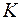 – приведенный модуль объемной упругости среды;
– приведенный модуль объемной упругости среды; 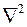 – оператор Лапласа. Пьезопроводность
– оператор Лапласа. Пьезопроводность 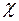 имеет размерность м2/с.
имеет размерность м2/с.
Если 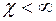
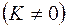 , то уравнение (2.33) описывает нестационарное поле давления при упругом режиме фильтрации. При
, то уравнение (2.33) описывает нестационарное поле давления при упругом режиме фильтрации. При 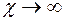
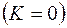 имеем уравнение Лапласа
имеем уравнение Лапласа
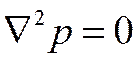 , ,
| (2.34) |
которое характеризует неупругий (жесткий) режим фильтрации и, следовательно, стационарное поле давления. Это же уравнение имеет место при 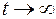 , т. е. при установившемся режиме фильтрации.
, т. е. при установившемся режиме фильтрации.
Для однозначного определения поля давления 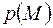 в заданной области
в заданной области 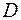 , ограниченной поверхностью
, ограниченной поверхностью 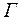 , необходимо и достаточно, чтобы решение уравнения (2.33) удовлетворяло начальному условию (при
, необходимо и достаточно, чтобы решение уравнения (2.33) удовлетворяло начальному условию (при 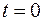 )
)
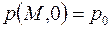 при при 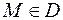
| (2.35) |
и при 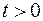 граничным условиям:
граничным условиям:
если на поверхности 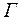 (или ее части) задано давление
(или ее части) задано давление 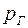 , то
, то
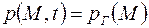 при при 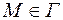 , ,
| (2.36) |
если задана нормальная составляющая скорости фильтрации, то
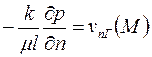 , ,
| (2.37) |
если поверхность 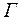 покрыта тонкой слабопроницаемой перемычкой (например, глинистая корка на стенке скважины), то
покрыта тонкой слабопроницаемой перемычкой (например, глинистая корка на стенке скважины), то
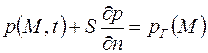 , ,
| (2.38) |
где 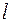 – характерный линейный размер;
– характерный линейный размер; 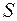 – коэффициент поверхностного фильтрационного сопротивления, получивший название параметр «скин-эффекта».
– коэффициент поверхностного фильтрационного сопротивления, получивший название параметр «скин-эффекта».
Ясно, что для уравнения (2.34) начальное условие (2.35) смысла не имеет, а граничные условия вида (2.36) – (2.38) сохраняются.
2. Модель ламинарной фильтрации ньютоновских однородных жидкостей для анизотропной среды.
Проницаемость зависит от направления - имеет место обобщенный закон Дарси
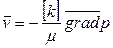 , ,
| (2.39) |
где 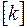 – тензор проницаемости.
– тензор проницаемости.
Если воспользоваться системой координат, оси которой совпадают с главными осями тензора 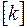 , то уравнение (2.39) в проекциях на оси декартовой системы координат перепишется в виде
, то уравнение (2.39) в проекциях на оси декартовой системы координат перепишется в виде
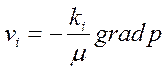 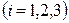 , ,
| (2.40) |
где 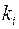 – проницаемости вдоль главных осей
– проницаемости вдоль главных осей 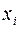 анизотропии. При этом проекция скорости фильтрации на нормаль к элементарной площадке вычисляется по формуле
анизотропии. При этом проекция скорости фильтрации на нормаль к элементарной площадке вычисляется по формуле
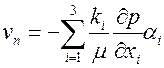 . .
| (2.41) |
Подставляя (2.40) в (2.32) получим уравнение при установившейся фильтрации
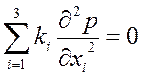 . .
| (2.42) |
Учитывая (2.41), усложняются и граничные условия вида (2.37) и (2.38).
Однако граничную задачу, связанную с уравнением (2.42), легко свести к граничной задаче, связанной с уравнением Лапласа (2.34), если вести следующую замену переменных:
для пространства
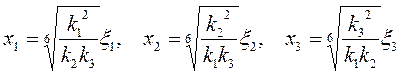
|
для плоскости
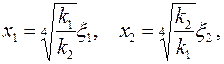
| (2.43) |
где 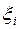 – новые координаты.
– новые координаты.
Это означает геометрическое преобразование анизотропной области 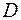 в некоторую изотропную область
в некоторую изотропную область 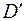 , проницаемость которой
, проницаемость которой
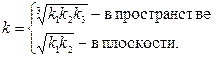
| (2.44) |
При этом граница 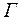 области
области 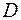 преобразуется в границу
преобразуется в границу 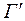 области
области 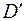 . Например, область, ограниченная окружностью
. Например, область, ограниченная окружностью
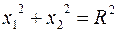 , ,
| (2.45) |
преобразуется согласно (2.42) в область, ограниченную эллипсом
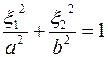 . .
| (2.46) |
или в параметрическом виде
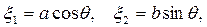 . .
|
где 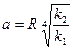 ,
, 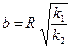 - полуоси элипса
- полуоси элипса
Для области 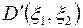 имеем уравнение Лапласа
имеем уравнение Лапласа
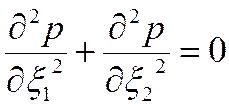 , ,
|
решение которого должно удовлетворять заданному граничному условию на окружности (2.45) для соответствующих точек эллипса (2.46).
3.Закономерности фильтрации жидкости в трещиновато-пористых пластах для однородной и изотропной среды.
Горная порода рассматривается как сплошная, в любой точке которой имеют место двойная пористость 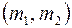 , проницаемость
, проницаемость 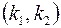 , скорость фильтрации
, скорость фильтрации 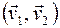 и давление
и давление 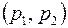 , связанные законом Дарси
, связанные законом Дарси
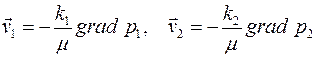
| (2.47) |
и уравнениями неразрывности
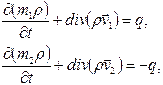
| (2.48) |
где индексами 1 и 2 обозначены величины, характеризующие соответственно систему трещин и пор;
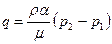 . .
| (2.49) |
– интенсивность перетока жидкости между этими системами; 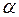 – новая безразмерная величина, характеризующая данную среду.
– новая безразмерная величина, характеризующая данную среду.
При этом пористости 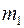 и
и 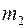 являются функциями обоих давлений, т.е.
являются функциями обоих давлений, т.е.
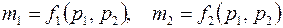 . .
| (2.50) |
Однако во многих случаях систему уравнений (2.47) – (2.48) можно упростить, если исходить из следующих условий:
а) объем, занимаемый трещинами, много меньше объема пор, т.е. допустимо принять 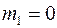 ;
;
б) изменение пористости 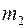 происходит в основном за счет изменения порового давления
происходит в основном за счет изменения порового давления 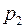 и поэтому при небольших изменениях этого давления
и поэтому при небольших изменениях этого давления
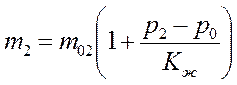 ; ;
| (2.51) |
в) проницаемость 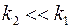 , т.е. фильтрацией в порах можно пренебречь
, т.е. фильтрацией в порах можно пренебречь 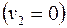 ;
;
г) жидкость слабосжимаема так что
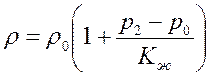 , ,
| (2.52) |
где 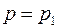 или
или 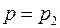 в зависимости от того, рассматривается жидкость в трещинах или в порах;
в зависимости от того, рассматривается жидкость в трещинах или в порах;
д) вязкость жидкости 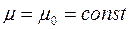 .
.
Физическая сущность перечисленных допущений состоит в том, что в системе трещины – поры рассматривается фильтрация жидкости по трещинам в условиях интенсивного массобмена с жидкостью, находящейся в упругом деформированном поровом пространстве.
В результате принятых упрощений уравнения (2.48) примут вид
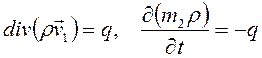 . .
|
Подставляя сюда соотношения (2.47), (2.49), (2.51), (2.52) и отбрасывая малые величины высших порядков, получим
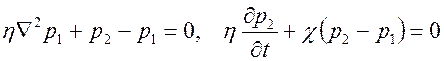 , ,
| (2.53) |
где 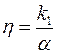 – специфическая характеристика трещиновато-пористой среды;
– специфическая характеристика трещиновато-пористой среды; 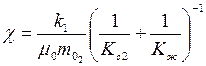 – своеобразная пьезопроводность среды.
– своеобразная пьезопроводность среды.
Параметр 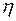 имеет размерность площади, и для реальных пород его порядок может изменяться в широких пределах – от 10-1 до 106 м2.
имеет размерность площади, и для реальных пород его порядок может изменяться в широких пределах – от 10-1 до 106 м2.
Легко заметить, что путем исключения одного из давлений система уравнений (2.53) сводится к одному уравнению
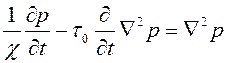 , ,
| (2.54) |
где 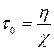 – параметр, называемый временем запаздывания.
– параметр, называемый временем запаздывания.
Это уравнение отличается от классического уравнения (2.33) слагаемым, содержащим параметр 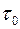 . В пределе, когда
. В пределе, когда 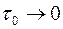 , среда с двойной пористостью переходит в чисто пористую и уравнения (2.54) и (2.33) совпадают.
, среда с двойной пористостью переходит в чисто пористую и уравнения (2.54) и (2.33) совпадают.
При жестком режиме фильтрации 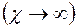 или при установившейся фильтрации
или при установившейся фильтрации 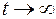 уравнение (2.54) обращается в уравнение Лапласа (2.34).
уравнение (2.54) обращается в уравнение Лапласа (2.34).
Следовательно, ставить задачу о фильтрации жидкости в трещиновато-пористой среде имеет смысл при 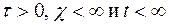 .
.
Начальное и граничные условия, которые необходимо присоединить к уравнению (2.54), обладают некоторой особенностью. Прежде всего ясно, что граничную задачу, связанную с уравнением (2.54) следует рассматривать относительно одного из давлений – 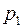 или
или 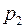 .
.
Если начальные условия 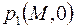 и
и 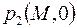 удовлетворяют первому уравнению (2.53), то задачу целесообразно решать относительно давления
удовлетворяют первому уравнению (2.53), то задачу целесообразно решать относительно давления 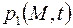 , принимая начальные и граничные условия в виде выражений (2.35) – (2.38). После определения давления
, принимая начальные и граничные условия в виде выражений (2.35) – (2.38). После определения давления 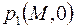 вычисляют поровое давление
вычисляют поровое давление 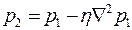 .
.
В противном случае задачу следует решать относительно давления 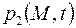 . Но здесь имеет место определенная специфика в задании граничных условий.
. Но здесь имеет место определенная специфика в задании граничных условий.
Если начальное распределение давления 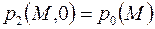 согласовано с граничными условиями
согласовано с граничными условиями 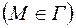 вида
вида
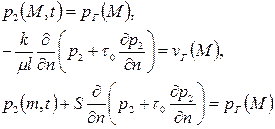 , ,
| (2.55) |
при 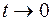 , то в таком виде граничная задача и рассматривается.
, то в таком виде граничная задача и рассматривается.
Но если же согласования нет, то к правым частям соответствующих граничных условий необходимо прибавить слагаемое 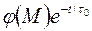 , где
, где 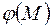 – невязка существующего граничного условия:
– невязка существующего граничного условия:
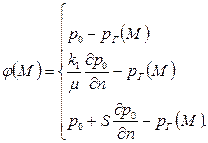
| (2.56) |
Это свидетельствует о том, что заданный скачок граничных условий в порах трещиновато-пористой среды не уничтожается мгновенно, как в обычной пористой среде, а убывает по закону 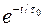 . Такое качественное отличие – результат принятого упрощения пренебрежения фильтрацией жидкости в порах, где давление изменяется только благодаря массообмену с жидкостью в трещинах. Аналогично, предположение о жестком характере фильтрации жидкости в трещинах приводит к указанной выше проверке начальных распределений давлений
. Такое качественное отличие – результат принятого упрощения пренебрежения фильтрацией жидкости в порах, где давление изменяется только благодаря массообмену с жидкостью в трещинах. Аналогично, предположение о жестком характере фильтрации жидкости в трещинах приводит к указанной выше проверке начальных распределений давлений 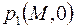 и
и 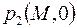 .
.
После решения граничной задачи относительно порового давления 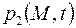 распределение давления
распределение давления 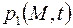 в трещинах определяется по формуле (2.53)
в трещинах определяется по формуле (2.53)
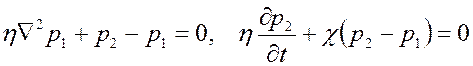
а скорости фильтрации относительно какой–либо поверхности – по формуле
(2.55)
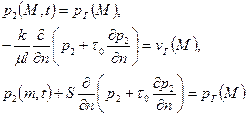
4. Приизучении фильтрации газа основное значение имеет его высокая сжимаемость, которая на несколько порядков выше сжимаемости пористой среды.
Поэтому в уравнении неразрывности (2.32) пренебрегают изменением пористости 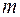 во времени и представляют это уравнение в виде
во времени и представляют это уравнение в виде
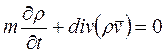 . .
| (2.57) |
К этому уравнению необходимо присоединить уравнение состояния газа
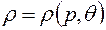
|
и закон фильтрации, который при небольшой скорости фильтрации имеет вид закона Дарси
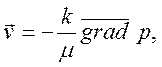
| (2.58) |
где в общем случае 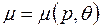 ;
; 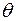 - температура.
- температура.
В простейшем случае газ можно считать термодинамически идеальным, находящемся при постоянной температуре 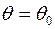 с вязкостью µ=const и плотностью
с вязкостью µ=const и плотностью
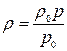 , ,
| (2.59) |
где 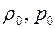 - постоянные величины.
- постоянные величины.
Подстановка (2.58) и (2.59) в (2.57) дает основное нелинейное уравнение теории фильтрации газа
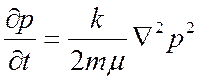 , ,
| (2.60) |
которое впервые было получено Л. С. Лейбензоном в 1930г.
Наиболее известный приближенный метод решения этого уравнения основан на линеаризации, по Л. С. Лейбензону, который состоит в том, что левую часть уравнения умножают на 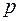 , а правую – на некоторое характерное давление
, а правую – на некоторое характерное давление 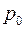 , например давление в невозмущенной части пласта.
, например давление в невозмущенной части пласта.
Тогда вместо (2.60) необходимо решить линейное уравнение
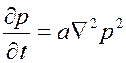 , ,
| (2.61) |
которое аналогично уравнению (2.33), где 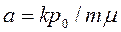 . Следовательно, все соотношения, полученные до сих пор для жидкости, могут быть в первом приближении использованы и при изучении фильтрации газа, если заменить в них
. Следовательно, все соотношения, полученные до сих пор для жидкости, могут быть в первом приближении использованы и при изучении фильтрации газа, если заменить в них 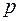 на
на 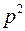 ,
, 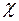 на
на 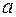 .
.
Лекция 4. 5. Экспериментально установлено, что иногда линейный закон фильтрации жидкости 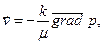 (2.58) нарушается и зависимость между
(2.58) нарушается и зависимость между 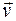 и
и 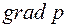 принимает вид выпуклой или вогнутой кривой, как показано на рис. 11.
принимает вид выпуклой или вогнутой кривой, как показано на рис. 11.
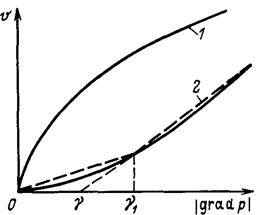
Рис. 11.Возможные виды нелинейного закона фильтрации
Основные причины проявления нелинейных эффектов следующие:
а) высокая скорость фильтрации, когда параметр Рейнольдса 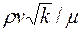 превышает критическое значение (зависимость изображена кривой 1 на рис. 11);
превышает критическое значение (зависимость изображена кривой 1 на рис. 11);
б) ламинарная фильтрация жидкостей с неньютоновскими свойствами (кривая 2);
в) малая скорость фильтрации в слабопроницаемых и неоднородных пластах (кривая 2).
Предложены различные аппроксимации нелинейных зависимостей. Например, кривая 1 чаще всего описывается двучленным законом фильтрации
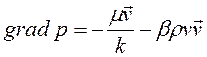 , ,
| (2.62) |
а кривая 2 – законом фильтрыции с предельным градиентом
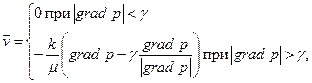
| (2.63) |
где, по данным Е. М. Минского, 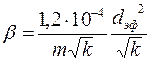 , а, по данным Б. И. Султанова,
, а, по данным Б. И. Султанова, 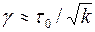 ;
; 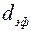 - эффективный диаметр пор;
- эффективный диаметр пор; 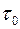 - предельное напряжение сдвига.
- предельное напряжение сдвига.
В общем случае к обоим типам кривых применимы степенная и кусочно-линейная аппроксимации
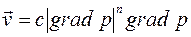 , ,
| (2.64) |
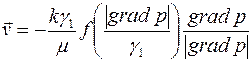 , ,
| (2.65) |
которыми удобно пользоваться при расчетах. Здесь 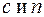 - параметры модели;
- параметры модели; 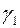 - характерное значение градиента давления;
- характерное значение градиента давления; 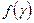 - безразмерная функция, описывающая ломаную линию (см. рис. 11).
- безразмерная функция, описывающая ломаную линию (см. рис. 11).
Дата добавления: 2015-09-28; просмотров: 1059;
