УРАВНЕНИЕ НЕРАЗРЫВНОСТИ

Один из фундаментальных законов ньютоновской механики материальных тел—это закон сохранения массы т любого индивидуального объема, т. е. объема, состоящего из одних и тех же частиц среды. Этот закон заключается в том, что для любого индивидуального объема т = const или в иной форме

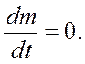
В механике сплошных сред почти всегда вместо массы рассматривается плотность ρ.

Для малого объема верно равенство Δm ≈ ρΔV, а для конечного объема — равенство 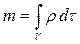, где интеграл взят по подвижному индивидуальному объему V.

Тогда закон сохранения массы т принимает вид

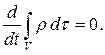(2.1)

Здесь не только плотность ρ — функция от координат точек пространства и времени, но и объем V зависит от t. Принимая это во внимание при вычислении производной в равенстве (2.1), несложно получить равенство

и так как оно справедливо для любого индивидуального объема, то получим первое основное дифференциальное уравнение механики сплошной среды

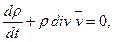(2.2)

которое называется уравнением неразрывности в переменных Эйлера. Это уравнение накладывает ограничение на скорость точек сплошной среды и применяется при больших перемещениях точек среды.

Если воспользоваться формулой (1.5), то уравнение (2.2) можно переписать в виде

(2.3)

В цилиндрической системе координат (r, Θ, z) при осевой симметрии 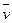= 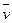(r, z) уравнение неразрывности принимает вид

Интересно, что уравнение (2.3) легко получить сразу, остава­ясь строго на точке зрения Эйлера. Для этого достаточно рассмотреть поток вектора ρ 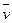сквозь некоторую неподвижную замкнутую поверхность S произвольной формы. Нам известно [см. формулу (1.10)], что этот поток может быть представлен в виде

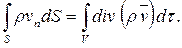
Он выражает массу среды, вытекающую за единицу времени из замкнутой поверхности S. Так как это повлечет за собой уменьшение плотности внутри S в единицу времени, равное (- dρ/dt), и соответственно изменение массы среды внутри S, равное

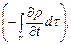то

Отсюда следует уравнение (2.3).

Для несжимаемой жидкости dρ/dt (хотя ∂ρ/∂t≠0),уравнение неразрывности (2.2) приобретает вид

div =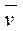

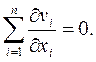
В этом случае поток скорости через любую неподвижную замкнутую поверхность равен нулю, т. е. объем втекающей жидкости равен объему вытекающей. Применяя это свойство к замкнутой поверхности, образованной трубкой тока и ее нормаль­ными сечениями, получим

v₁S₁=v₂S₂ .

Конечно, не существует сред, в строгом смысле действительно несжимаемых, однако весьма часто в инженерной практике предположение о постоянстве ρ приводит к значительному упрощению задачи и почти не вносит ошибки.

Для стационарных движений ∂ρ/∂t = O, уравнение неразрыв­ности получает вид

div ρ 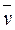= 0или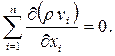

Уравнение (2.2) или (2.3) справедливо для любой однородной сплошной среды, когда нет поглощений массы, химических реакций, внутренней диффузии и других процессов, связанных с влиянием окружающих тел. Однако оно легко обобщается для многокомпонентных смесей или многофазных сред с учетом различного взаимного влияния компонентов (или фаз).

Для этого всякий индивидуальный объем можно представить как совокупность п континуумов, каждый из которых имеет свою плотность ρ_1, ρ₂, ..., ρ_n и свою скорость 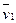, , …, 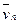. Если в смеси не происходит химических реакций и других процессов взаимных превращений, то для каждого компонента смеси должен выпол­няться закон сохранения массы

или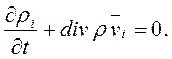

Если же в смеси происходят химические реакции, то массы компонентов т_i могут меняться. Пусть γ_i — изменение массы т_i i-го компонента смеси в единицу времени на единицу объема за счет химической реакции. Тогда уравнение неразрывности для компонента смеси можно записать в виде

или (2.4)

Согласно закону сохранения общей массы при химических реакциях имеем

(2.5)

Кроме п плотностей и п скоростей для компонентов смеси можно ввести одну плотность ρ и одну скорость 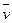смеси как целого.

Для этого достаточно просуммировать уравнения (2.4), учесть (2.5) и получим следующие равенства

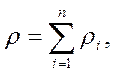
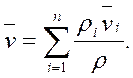
В результате уравнение неразрывности примет обычный вид (2.3) относительно средних характеристик среды.

Все сказанное остается в силе, если вместо химических реакций в многокомпонентных смесях рассматриваются процессы взаимных поглощений (или выделений) в многофазных средах. В этом случае в формуле (2.4) γ_i — интенсивность поглощения i-той фазы среды.

§ 2. УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ

Известно, что основным динамическим уравнением движения материальной точки является второй закон Ньютона ma = R, a широко используемыми следствиями этого закона являются сле­дующие общие теоремы движения системы материальных точек:

а) производная по времени от количества движения

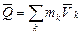
системы равна сумме всех действующих на систему внешних сил

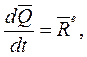(2.6)

и называется уравнением количества движения или уравнением импульсов:

(2.6')

б) производная по времени от кинетического момента

системы относительно какого-либо неподвижного центра О равна сумме моментов всех внешних сил, действующих на систему, относительно того же центра, т. е.

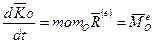(2.7)

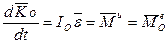
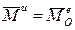
называется уравнением моментов количества движения или просто