Приток газа к скважине по закону Дарси

Исследуем установившийся плоскорадиальный фильтрационный поток идеального газа. Для этого воспользуемся аналогией между фильтрацией несжимаемой жидкости и газа. Запишем формулу дебита совершенной скважины для несжимаемой жидкости:

.

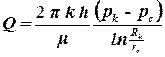(3.17)

Произведем в этом уравнении замены. Заменим давление p на функцию Лейбензона P, а объемный расход Q на массовый расход Q_m.

.

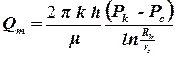(3.18)

В последней формуле распишем функцию Лейбензона, тогда массовый дебит газовой скважины будет рассчитываться по формуле:

,

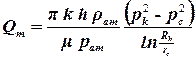(3.19)

а приведенный к атмосферным условиям объемный расход

.

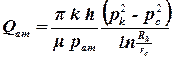(3.20)

Расчет распределения давления вокруг газовой скважины производится в той же последовательности:

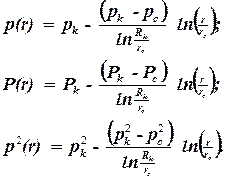
(3.21)

Скорости фильтрации в любой точки вокруг скважины можно найти из уравнения неразрывности:

.

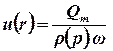(3.22)

На Рис. 3.2.a, и b приведены распределение давления и скорости фильтрации вокруг газовой скважины. У газовой скважины падение давления вблизи скважины больше, чем у нефтяной, поэтому при прочих равных условиях и скорости фильтрации у газовой скважины уменьшается быстрее, чем у нефтяной скважины.

Рис. 3.2 . Распределение давления a) и отношение скорости фильтрации в пласте к скорости фильтрации на скважине б) для газовой скважины