Приток к галерее в зонально–неоднородном пласте

Рис. 2.9 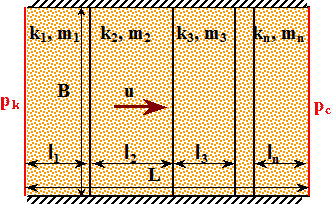. Схема зонально-неоднородной галереи

Пусть горизонтальный пласт постоянной толщиной h и шириной B имеет проницаемость, которая меняется вдоль направления фильтрации несжимаемой жидкости оси x. Давление на контуре питания и галерее p_k и p_г, длина L. Необходимо рассчитать дебит скважины и распределение давления по длине галереи.

При фильтрации несжимаемой жидкости объемный расход через любое поперечное сечение будет одинаковым. Считая, что фильтрация происходит по закону Дарси, запишем:

.

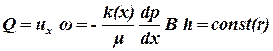(2.54)

Разделяя переменные в этом уравнении, получим:

.

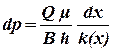(2.55)

Интегрируя полученное уравнение по давлению от p_г до p(x), а по длине галереи x_г до x найдем распределение давления по пласту

.

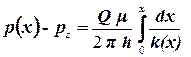(2.56)

Для нахождения расхода подставим в уравнение (2.50) граничное условие x = L, p(L) = p_k и найдем дебит скважины:

.

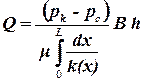(2.57)

Будем считать, что этот неоднородный пласт является однородным пластом с проницаемостью k_ср. Тогда дебит такого пласта определяться по формуле:

.

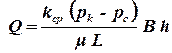(2.58)

Сравнивая формулы для неоднородного и однородного пласта можно найти среднюю проницаемость

.

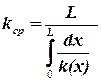(2.59)

Рассмотрим частный случай, когда пласт вокруг скважины состоящий из n зон. Длина i – той зоны ℓ_i, проницаемостью k_i. Тогда интеграл в формуле расчета средней проницаемости можно разбить на сумму интегралов по каждой зоне, которые вычисляются:

.

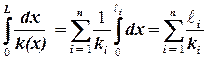(2.60)

В этом случае среднюю проницаемость удобно рассчитать по формуле:

.

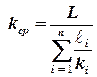(2.61)

а давление на внешней границе j – той зоны

.

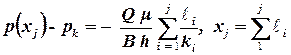(2.62)

Последнюю формулу удобно использовать, если заданы дебиты и давление на галерее. Если же заданы давления на галерее и контуре питания, то из последней формулы удобно исключить дебит Q, тогда получим:

.

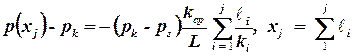(2.63)

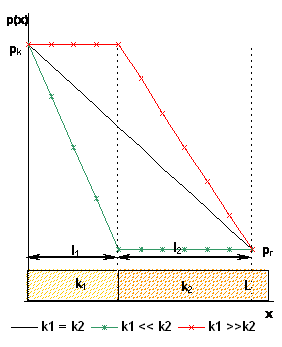
На Рис. 2.10 показано распределение давления по длине галереи состоящей из двух пропластков с проницаемостями k₁ и k₂ для однородного пласта и двух предельных случаев неоднородного пласта.

Рис. 2.10. Предельные случаи распределение давления по галерее в зонально-неоднородном пласте