Общие теоретические сведения

Интегратором называется устройство, выходной сигнал которого пропорционален интегралу по времени от входного сигнала. Простейшая (идеальная) схема интегратора приведена на рис. 4.

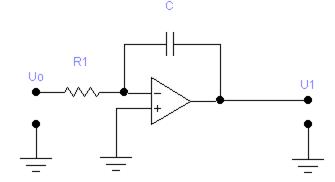
Рис. 4. Схема простейшего интегратора на ОУ.

В этой схеме в цепь обратной связи ОУ включен конденсатор, сопротивление которого велико для низкочастотных составляющих спектра выходного сигнала и мало для высокочастотных. В результате коэффициент усиления ОУ становится переменным для различных частот спектра сигнала. По первому закону Кирхгофа для инвертирующего входа ОУ можно записать

Uo/R1 = - C∙dU1/dt.

При записи этого соотношения предполагаем, что начальные условия – нулевые ( Uo = U1 = 0 при t = 0), а ОУ – идеальный (K_U = ∞, R_вх = ∞ ).

Приведенную выше формулу можно записать так

Полученный результат справедлив только для идеального ОУ. Для реального интегратора эта формула является приближенной. Так, на точность работы реального интегратора влияют дрейфовые составляющие входного сигнала, которые необходимо скомпенсировать или ослабить. Для этого обычно параллельно конденсатору С в схеме на рис. 3 включают резистор R2 с большим сопротивлением (рис. 5). В результате применения отрицательной обратной связи по постоянному току обеспечивается стабилизация рабочей точки ОУ и предотвращается полный заряд конденсатора С.

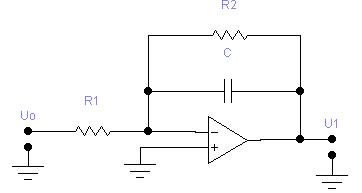
Рис. 5. Схема интегратора с дополнительным резистором в обратной связи.

Если на вход этой схемы подать скачок напряжения величиной Uo, то выходное напряжение U1 в ней изменяется в соответствии с выражением

Анализ этого выражения показывает, что на начальном участке переходного процесса (при малом времени интегрирования) характеристика интегратора близка к идеальной.

Исходные данные:

· ОУ LM 741.

· R1=100 КоМ

· R2=100 КоМ

· C=0,03 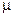F

Задача исследования:

· Получить осциллограммы переходного процесса интегратора при подаче на вход напряжения в виде последовательности прямоугольных импульсов.

Схема исследованияинтегратора на ОУ, представлена на рис. 6.

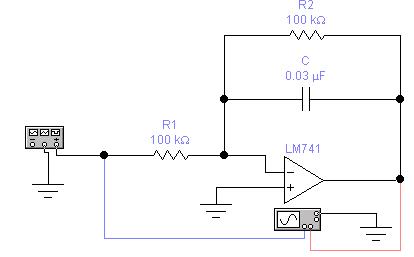
Рис. 6.