Сопряжения.

Плавный переход одной линии в другую называется касанием. Прямая, касательная к окружности, образует прямой угол с радиусом, проведенным в точку касания (рис. 2.36). Геометрическим местом центров окружностей, касательных к данной прямой, являются две прямые MN и PQ, параллельные АВ и удаленные от нее на расстояние R (рис. 2.37). Любую точку прямых MN и PQ можно принять за центр окружности, касательной к АВ. Точка касания К – основание перпендикуляра, опущенного из центра 0 на прямую АВ.

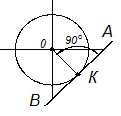Рис. 2.36

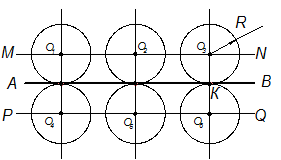Рис. 2.37

Касание бывает внешнее и внутреннее. При внешнем касании расстояние между центрами окружностей равно сумме их радиусов R₁ + R₂ и точка касания расположена на линии центров между точками 0₁ и 0₂. Окружности лежат по разные стороны от касательной t (рис. 2.38). При внутреннем касании расстояние между центрами окружностей равно разности радиусов R₁ – R₂ и точка касания находится на линии центров за точками 0₁ и 0₂. Окружности лежат по одну сторону от касательной t (рис. 2.39), t – общая касательная, перпендикулярная к радиусам, проведенным в эту точку.

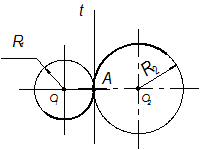Рис. 2.38

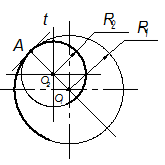Рис. 2.39

Сопряжением называется плавный переход одной линии в другую, выполненный при помощи промежуточной линии (дуги сопряжения).

Основными элементами сопряжения являются: - R – радиус дуги сопряжения - О – центр сопряжения - А и В – точки сопряжения.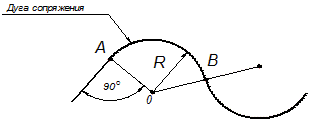

Рис. 2.40