Циклічні процеси. Теплові машини
Коловим, або циклічним, процесом називають процес, за якого система повертається в початковий стан через низку проміжних станів.
У координатах рV циклічний процес зображають замкненою кривою (рис. 3.6). Якщо під час циклічного процесу виконана робота додатна ( 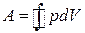 >0), то цикл називають прямим (див. рис. 3.6, а). Якщо ж А<0, то цикл обернений (див. рис. 3.6, б).
>0), то цикл називають прямим (див. рис. 3.6, а). Якщо ж А<0, то цикл обернений (див. рис. 3.6, б).
 |
У термодинаміці розглядають оборотні й необоротні процеси. Оборотним називають процес, який може відбуватися і в прямому, і в оберненому напрямі, однак у цьому разі в навколишньому середовищі не простежується ніяких змін. Реальні циклічні процеси переважно супроводжуються дисипацією енергії, тому вони є необоротними. Оборотний процес – це ідеалізація реального процесу, тобто корисна ідеалізація, оскільки робота практично всіх теплових машин ґрунтується на циклічних процесах, що наближені до оборотних. Зокрема, в теплових двигунах, які виконують роботу завдяки отриманій теплоті, відбувається прямий оборотний цикл, а в холодильних пристроях – обернений.
 Теплова машина – це пристрій для перетворення теплової енергії в механічну. У складі теплової машини є нагрівник, холодильник і робоче тіло (рис. 3.7).
Теплова машина – це пристрій для перетворення теплової енергії в механічну. У складі теплової машини є нагрівник, холодильник і робоче тіло (рис. 3.7).
Внутрішня енергія U є функцією стану термодинамічної системи. Отже, для циклічного процесу ΔU=0, оскільки система завжди повертається в початковий стан. За цих умов, згідно з першим законом термодинаміки, Q=A, де Q – кількість теплоти, отримана системою за повний цикл; А – робота системи протягом циклу.
 Розглянемо прямий оборотний циклічний процес, що відбувається з ідеальним газом і складається з чотирьох оборотних процесів: двох адіабатних і двох ізотермічних. Такий процес називають циклом Карно (рис. 3.8). Під час ізотерміч-ного розширення 1–2 газ отримує теплоту Q1 від нагрівника, після чого його розширення відбувається адіабатно 2–3. В наступних етапах циклу відбувається ізотермічне стискання газу 3–4, під час якого газ віддає частину теплоти Q2 холодильнику. Завершує цикл адіабатне стискання 4–1, після якого газ повертається до початкового стану. Виконана газом протягом циклу корисна робота Ак відповідає заштрихованій площі на рис. 3.8.
Розглянемо прямий оборотний циклічний процес, що відбувається з ідеальним газом і складається з чотирьох оборотних процесів: двох адіабатних і двох ізотермічних. Такий процес називають циклом Карно (рис. 3.8). Під час ізотерміч-ного розширення 1–2 газ отримує теплоту Q1 від нагрівника, після чого його розширення відбувається адіабатно 2–3. В наступних етапах циклу відбувається ізотермічне стискання газу 3–4, під час якого газ віддає частину теплоти Q2 холодильнику. Завершує цикл адіабатне стискання 4–1, після якого газ повертається до початкового стану. Виконана газом протягом циклу корисна робота Ак відповідає заштрихованій площі на рис. 3.8.
Головною характеристикою будь-якого оборотного циклу є його коефіцієнт корисної дії η, який визначають як відношення корисної роботи Ак до кількості теплоти Q1, яку система отримує від нагрівника протягом циклу:

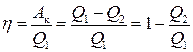 . (3.65)
. (3.65)
У координатах ТS цикл Карно має інший вигляд (рис. 3.9). Цим графіком зручно скористатись, щоб вивести іншу формулу для к.к.д. циклу Карно. Зокрема, корисній роботі Ак на графіку відповідає заштрихована площа 1–2–3–4, отже,
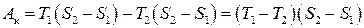 . (3.66)
. (3.66)
Кількості теплоти Q1 відповідає площа прямокутника 1–2 –S2–S1:
Q1=T1(S2–S1). (3.67)
Тоді на підставі (3.65) – (3.67) отримаємо
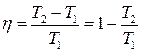 , (3.68)
, (3.68)
де Т1, Т2 – температури нагрівника і холодильника, відповідно. Зазначимо, що співвідношення (3.68), на відміну від (3.65), застосовне лише для оборотного циклу Карно.
Ми довели одне з важливих положень термодинаміки – першу теорему Карно, яка твердить, що к.к.д. циклу Карно не залежить від природи робочого тіла, а визначений лише температурами нагрівника і холодильника.
Друга теорема Карно стверджує, що к.к.д. необоротного циклу Карно не може перевищувати к.к.д. оборотного циклу Карно, якщо в обох циклах нагрівник і холодильник є спільними.
Отже, на підставі другої теореми Карно
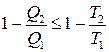 або
або 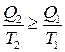 . (3.69)
. (3.69)
Співвідношення (3.69) – це нерівність Клаузіуса для циклу Карно. Якщо узагальнити (3.69), то для будь-якого циклу можна довести, що 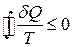 або, ввівши ентропію S,
або, ввівши ентропію S,
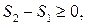 тобто ΔS
тобто ΔS 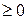 . (3.70)
. (3.70)
Співвідношення (3.70) є одним з виразів другого закону термодинаміки: в ізольованих системах усі фізичні процеси не супроводжуються зменшенням ентропії. Якщо процес оборотний, то ΔS=0, тобто ентропія системи є сталою. За умови необоротного процесу ΔS>0, тобто ентропія системи зростає.
Є ще кілька формулювань другого закону термодинаміки.
1. Неможливий процес, єдиний результат якого – передавання теплоти від менш нагрітого тіла до більш нагрітого (Р. Клаузіус).
2. Неможливий процес, єдиним результатом якого є виконання роботи лише внаслідок охолодження одного тіла (У. Томсон).
Неважко довести, що всі три формулювання другого закону термодинаміки еквівалентні.
Дата добавления: 2015-09-02; просмотров: 1137;
