Теоретическое введение. Дисперсией света называется зависимость показателя преломления n вещества от частоты n (длины волны l) света или фазовой скорости v световых волн от его
Дисперсией света называется зависимость показателя преломления n вещества от частоты n (длины волны l) света или фазовой скорости v световых волн от его частоты n.
 |
Дисперсия света представляется в виде зависимости:
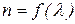 ;
; 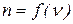 . Первое экспериментальное исследование дисперсии света было выполнении Ньютоном в 1672 г. Следствием дисперсии является разложение в спектр белого света при прохождении его через призму (рис.5.1). После прохождения света через призму образуется спектр, в котором линии каждой частоты (длины волны) занимают совершенно определенное место. Величина
. Первое экспериментальное исследование дисперсии света было выполнении Ньютоном в 1672 г. Следствием дисперсии является разложение в спектр белого света при прохождении его через призму (рис.5.1). После прохождения света через призму образуется спектр, в котором линии каждой частоты (длины волны) занимают совершенно определенное место. Величина
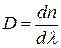 , (5.1)
, (5.1)
называемая дисперсией вещества, показывает, как быстро изменяется показатель преломления с длиной волны. Различают два вида дисперсии: нормальную (D<0), при которой показатель преломления монотонно увеличивается с ростом частоты; и аномальную (D>0), при которой показатель преломления уменьшается с увеличением частоты. Для всех прозрачных бесцветных веществ в видимой части спектра дисперсия нормальная (участки 1-2 и 3-4 на рис. 5.2). Если вещество поглощает свет в каком-то диапазоне длин волн (частот), то в области поглощения дисперсия оказывается аномальной (участок 2-3 рис. 5.2).
Из электромагнитной теории Максвелла известно, что фазовая скорость электромагнитных волн равна
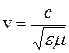 , (5.2)
, (5.2)
где c – скорость света в вакууме; e – диэлектрическая проницаемость среды; m – магнитная проницаемость среды. Для большинства прозрачных сред m=1, следовательно,
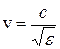 ;
; 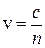 ;
; 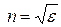 . (5.3)
. (5.3)
Однако из последнего соотношения выявляются некоторые противоречия: 1) n – переменная величина, а e – постоянная для данного вещества; 2) значения n не согласуются с опытными значениями: для воды n≈1.33, а e=81.
Трудности объяснения дисперсии с точки зрения электромагнитной теории Максвелла устраняются электронной теорией Лоренца. В теории Ло‑
ренца дисперсия света рассматривается как результат взаимодействия электро‑
магнитных волн с веществом. Движение электронов в атоме подчиняется законам квантовой механики. В частности, понятие траектории электрона в атоме теряет всякий смысл. Однако, как показал Лоренц, для качественного понимания многих оптических явлений достаточно ограничиться гипотезой о существовании внутри атомов и молекул электронов, связанных квазиупруго. Будучи выведены из положения равновесия, такие электроны начнут колебаться, постепенно теряя энергию колебаний на излучение электромагнит‑
ных волн. В результате колебания будут затухающими. Затухание можно учесть, введя «силу трения», пропорциональную скорости.
Электромагнитная волна, в которой вектор напряжённости электрического поля изменяется по закону:
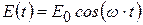 , (5.4)
, (5.4)
проходя через вещество, действует на каждый электрон с силой:
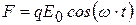 , (5.5)
, (5.5)
где Е0 – амплитуда напряжённости электрического поля волны.
Исходя из второго закона Ньютона, можно записать дифференциальное уравнение колебаний электрона:
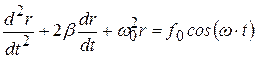 , (5.6)
, (5.6)
где r – смещение электрона из положения равновесия, β – коэффициент затухания, ω0 – собственная частота колебаний электрона, 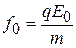 . Под воздействием силы (5.5) электрон совершает вынужденные колебания:
. Под воздействием силы (5.5) электрон совершает вынужденные колебания:
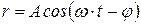 , (5.7)
, (5.7)
амплитуда А и фаза j которых определяются формулами:
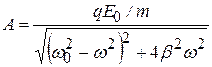 ;
; 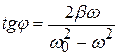 . (5.8)
. (5.8)
Колеблющийся электрон возбуждает вторичную волну, распространяющуюся со скоростью с. Вторичные волны, складываясь с первичной, образуют результирующую волну. Фазы вторичных волн отличаются от фазы первичной волны. Это приводит к тому, что результирующая волна распространяется в веществе с фазовой скоростью v, отличной от скорости волн в вакууме. Различие между v и с будет тем больше, чем сильнее вынужденные колебания электронов (то есть чем ближе частота волны к резонансной частоте электронов). Отсюда вытекает существование зависимости v от ω.
Чтобы упростить вычисления, затуханием за счёт излучения вначале будем пренебрегать (β=0), тогда из (5.8) получим:
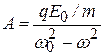 ;
; 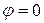 . (5.10)
. (5.10)
Таким образом, при отсутствии затухания электрон будет совершать под действием силы (5.5) колебания, описываемые формулой:
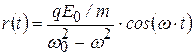 .
.
С учётом (5.4):
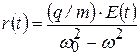 .
.
В результате смещения электронов из положений равновесия молекула приобретёт электрический дипольный момент:
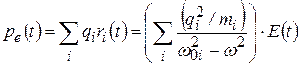 . (5.11)
. (5.11)
Здесь предполагается, что каждый атом (или молекулу) вещества можно рассматривать как систему нескольких гармонических осцилляторов – заряженных частиц с различными эффективными зарядами qi и массами mi, частоты собственных незатухающих колебаний которых равны 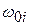 . Все эти осцилляторы смещаются под действием электрического поля волны и вносят свой вклад в поляризацию вещества. Суммирование в (5.11) производится по всем осцилляторам (оптическим электронам), входящим в состав молекулы. Обозначим N – число молекул в единице объёма вещества, тогда мгновенное значение вектора поляризации вещества:
. Все эти осцилляторы смещаются под действием электрического поля волны и вносят свой вклад в поляризацию вещества. Суммирование в (5.11) производится по всем осцилляторам (оптическим электронам), входящим в состав молекулы. Обозначим N – число молекул в единице объёма вещества, тогда мгновенное значение вектора поляризации вещества:
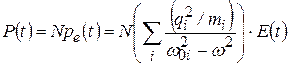 . (5.12)
. (5.12)
Диэлектрическая проницаемость вещества связана с диэлектрической восприимчивостью 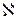 :
:
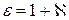 , (5.13)
, (5.13)
а величина вектора поляризации:
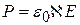 , (5.14)
, (5.14)
тогда из (5.3), (5.12-5.14):
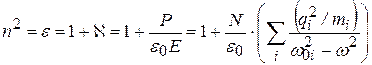 . (5.15)
. (5.15)
 При значениях частоты волны ω, заметно отличающихся от всех собственных частот
При значениях частоты волны ω, заметно отличающихся от всех собственных частот 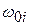 , сумма в (5.15) будет мала по сравнению с единицей, так что
, сумма в (5.15) будет мала по сравнению с единицей, так что 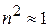 . Вблизи каждой из собственных частот функция (5.15) терпит разрыв: при ω→
. Вблизи каждой из собственных частот функция (5.15) терпит разрыв: при ω→ 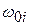 она обращается в
она обращается в 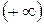 , если ω<
, если ω< 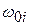 , и в
, и в 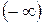 , если ω>
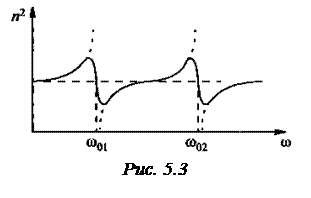
, если ω> 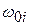 . Такое поведение функции обусловлено тем, что мы пренебрегли затуханием: положили β=0. Когда β отлично от нуля, функция (5.15) при всех значениях ω остаётся конечной. На рис. 5.3 показан ход функции (5.15) без учёта затухания (пунктир) и зависимость n2=f(ω) с учётом затухания (сплошная кривая). Перейдя от частот к длинам волн, получим кривую, изображённую на рис.5.2.
. Такое поведение функции обусловлено тем, что мы пренебрегли затуханием: положили β=0. Когда β отлично от нуля, функция (5.15) при всех значениях ω остаётся конечной. На рис. 5.3 показан ход функции (5.15) без учёта затухания (пунктир) и зависимость n2=f(ω) с учётом затухания (сплошная кривая). Перейдя от частот к длинам волн, получим кривую, изображённую на рис.5.2.
Таким образом, в областях частот, близким к собственным частотам электронов 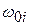 , имеет место аномальная дисперсия, а в остальных областях – нормальная. Области аномальной дисперсии являются резонансными областями. При резонансе за счёт вынуждающей силы (5.5) амплитуда вынужденных колебаний максимальна, при этом обеспечивается максимальная скорость поступления энергии в систему, световая волна поглощается. Таким образом, области аномальной дисперсии, вследствие их резонансного характера, являются областями поглощения. На рис.5.2. пунктирная кривая изображает ход коэффициента поглощения света веществом.
, имеет место аномальная дисперсия, а в остальных областях – нормальная. Области аномальной дисперсии являются резонансными областями. При резонансе за счёт вынуждающей силы (5.5) амплитуда вынужденных колебаний максимальна, при этом обеспечивается максимальная скорость поступления энергии в систему, световая волна поглощается. Таким образом, области аномальной дисперсии, вследствие их резонансного характера, являются областями поглощения. На рис.5.2. пунктирная кривая изображает ход коэффициента поглощения света веществом.
Элементарная теория дисперсии Лоренца не только позволила объяснить нормальную и аномальную дисперсию, но избирательность поглощения света на различных частотах.
Дата добавления: 2015-09-07; просмотров: 1364;
