Теоретическое введение. Линейно поляризованный свет
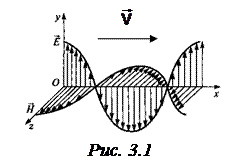 Линейно поляризованный свет. Следствием теории Максвелла является поперечность световых волн: векторы напряженности электрического
Линейно поляризованный свет. Следствием теории Максвелла является поперечность световых волн: векторы напряженности электрического 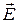 и магнитного
и магнитного 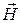 полей волны взаимно перпендикулярны и колеблются перпендикулярно вектору скорости
полей волны взаимно перпендикулярны и колеблются перпендикулярно вектору скорости 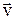 распространения волны (рис.3.1). При рассмотрении поляризации обычно все рассуждения связывают с плоскостью колебаний вектора напряженности электрического поля
распространения волны (рис.3.1). При рассмотрении поляризации обычно все рассуждения связывают с плоскостью колебаний вектора напряженности электрического поля 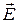 –светового вектора, так как химическое, физиологическое и другие виды воздействия света на вещество обусловлены главным образом электрическими колебаниями.
–светового вектора, так как химическое, физиологическое и другие виды воздействия света на вещество обусловлены главным образом электрическими колебаниями.
 Электромагнитная волна от отдельного элементарного излучателя (атома, молекулы) всегда поляризована. В свете, испускаемом обычными источниками, имеются колебания, совершающиеся в различных направлениях, перпендикулярных к лучу. В таких световых волнах, исходящих из различных элементарных излучателей (атомов), векторы
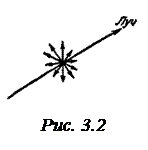
Электромагнитная волна от отдельного элементарного излучателя (атома, молекулы) всегда поляризована. В свете, испускаемом обычными источниками, имеются колебания, совершающиеся в различных направлениях, перпендикулярных к лучу. В таких световых волнах, исходящих из различных элементарных излучателей (атомов), векторы 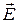 имеют различные ориентации, причем все эти ориентации равновероятны, что обусловлено большим числом атомных излучателей. Такой свет называется естественным, или неполяризованным (рис.3.2).
имеют различные ориентации, причем все эти ориентации равновероятны, что обусловлено большим числом атомных излучателей. Такой свет называется естественным, или неполяризованным (рис.3.2).
Из пучка естественного света можно выделить часть, в которой колебания вектора 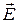 будут происходить в одном определенном направлении в плоскости, перпендикулярной лучу, т.е. выделенный свет будет линейно поляризованным. Плоскость, в которой колеблется световой вектор (то есть вектор напряжённости электрического поля
будут происходить в одном определенном направлении в плоскости, перпендикулярной лучу, т.е. выделенный свет будет линейно поляризованным. Плоскость, в которой колеблется световой вектор (то есть вектор напряжённости электрического поля 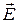 ), называется плоскостью колебаний. По историческим причинам плоскостью поляризации была названа не плоскость, в которой колеблется вектор
), называется плоскостью колебаний. По историческим причинам плоскостью поляризации была названа не плоскость, в которой колеблется вектор 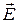 , а перпендикулярная к ней плоскость.
, а перпендикулярная к ней плоскость.
Закон Малюса. Плоскополяризованный свет можно получить из естественного с помощью приборов, называемых поляризаторами. Эти приборы свободно пропускают колебания, параллельные плоскости, которая называется главной плоскостью поляризатора, и полностью задерживают колебания, перпендикулярные к этой плоскости. Колебание амплитуды E0, совершающееся в плоскости, образующей угол φ с главной плоскостью поляризатора, можно разложить на два колебания с амплитудами
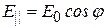 (3.1)
(3.1)
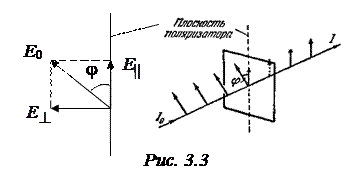 и
и 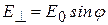 (рис. 3.3). Первое колебание пройдёт через прибор, второе будет задержано. Интенсивность волны пропорциональна квадрату её амплитуды:
(рис. 3.3). Первое колебание пройдёт через прибор, второе будет задержано. Интенсивность волны пропорциональна квадрату её амплитуды: 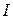 ~
~ 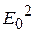 , поэтому из (3.1) получим:
, поэтому из (3.1) получим: 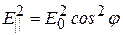 , или для интенсивности I прошедшей через поляризатор волны:
, или для интенсивности I прошедшей через поляризатор волны:
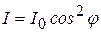 , (3.2)
, (3.2)
где I0 – интенсивность падающей на поляризатор линейно поляризованной волны, φ – угол между главной плоскостью поляризатора и плоскостью колебаний падающей волны.
Соотношение (3.2) носит название закона Малюса.
В естественном свете все значения φ равновероятны. Поэтому доля света, прошедшего через поляризатор, будет равна среднему значению 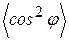 , т.е. ½:
, т.е. ½:
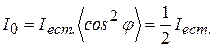 (3.3)
(3.3)
При вращении поляризатора вокруг направления естественного луча интенсивность прошедшего света остаётся одной и той же, изменяется лишь ориентация плоскости колебаний света, выходящего из прибора. 
Поставим на пути естественного луча два поляризатора, главные плоскости которых образуют угол φ. Из первого поляризатора выйдет плоскополяризованный свет, интенсивность которого 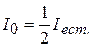 . Интенсивность света, вышедшего из второго поляризатора (его называют анализатором), согласно закону Малюса (3.2) равна:
. Интенсивность света, вышедшего из второго поляризатора (его называют анализатором), согласно закону Малюса (3.2) равна:
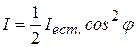 . (3.4)
. (3.4)
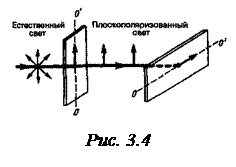
Максимальная интенсивность, равная Iест./2, получается при φ=0 (главные плоскости поляризаторов параллельны). При φ=π/2 интенсивность равна нулю – скрещенные поляризаторы света не пропускают (рис.3.4).
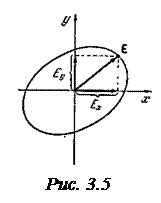
Эллиптическая поляризация. Рассмотрим две когерентные плоскополяризованные световые волны, плоскости колебаний которых взаимно перпендикулярны. Пусть колебания в одной волне совершаются вдоль оси х (рис.3.5), во второй – вдоль оси у (оси х и у лежат в перпендикулярной к лучу плоскости). Проекции световых векторов этих волн на соответствующие оси изменяются по закону:
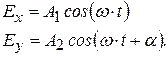 (3.6)
(3.6)
Величины Ех и Еу представляют собой координаты конца результирующего светового вектора 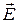 (см. рис. 3.5). Исключая переменную t, получим:
(см. рис. 3.5). Исключая переменную t, получим:
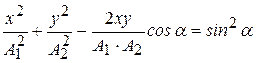 . (3.7)
. (3.7)
Это в общем случае уравнение эллипса. Таким образом, две когерентные плоскополяризованные световые волны, плоскости колебаний которых взаимно перпендикулярны, при наложении друг на друга дают волну, в которой световой вектор (вектор 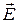 ) изменяется со временем так, что конец его описывает эллипс. Такой свет называется эллиптически поляризованным. При разности фаз
) изменяется со временем так, что конец его описывает эллипс. Такой свет называется эллиптически поляризованным. При разности фаз 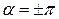 эллипс вырождается в прямую, и получается плоскополяризованный свет. При разности фаз
эллипс вырождается в прямую, и получается плоскополяризованный свет. При разности фаз 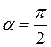 и равенстве амплитуд складываемых волн эллипс превращается в окружность. В этом случае получается свет, поляризованный по кругу. В зависимости от направления вращения вектора
и равенстве амплитуд складываемых волн эллипс превращается в окружность. В этом случае получается свет, поляризованный по кругу. В зависимости от направления вращения вектора 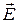 различают правую и левую эллиптическую и круговую поляризацию.
различают правую и левую эллиптическую и круговую поляризацию.
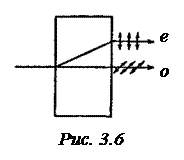 Поляризация при двойном лучепреломлении. При прохождении света через некоторые кристаллы световой луч разделяется на два луча. Это явление, получившее название двойного лучепреломления, было наблюдено в 1670 г. Эразмом Бартоломином для исландского шпата (разновидность углекислого кальция, СаСО3). При двойном лучепреломлений один из лучей удовлетворяет обычному закону преломления и лежит в одной плоскости с падающим лучом и нормалью. Этот луч называется обыкновенным и обозначается на чертежах буквой о. Для другого луча, называемого необыкновенным (его принято обозначать буквой е), отношение (sini1/sini2) не остается постоянным при изменении угла падения. Даже при нормальном падении необыкновенный луч, вообще говоря, отклоняется от первоначального направления (рис.3.6). Кроме того, необыкновенный луч не лежит, как правило, в одной плоскости с падающим лучом и нормалью к преломляющей поверхности.
Поляризация при двойном лучепреломлении. При прохождении света через некоторые кристаллы световой луч разделяется на два луча. Это явление, получившее название двойного лучепреломления, было наблюдено в 1670 г. Эразмом Бартоломином для исландского шпата (разновидность углекислого кальция, СаСО3). При двойном лучепреломлений один из лучей удовлетворяет обычному закону преломления и лежит в одной плоскости с падающим лучом и нормалью. Этот луч называется обыкновенным и обозначается на чертежах буквой о. Для другого луча, называемого необыкновенным (его принято обозначать буквой е), отношение (sini1/sini2) не остается постоянным при изменении угла падения. Даже при нормальном падении необыкновенный луч, вообще говоря, отклоняется от первоначального направления (рис.3.6). Кроме того, необыкновенный луч не лежит, как правило, в одной плоскости с падающим лучом и нормалью к преломляющей поверхности.
Явление двойного лучепреломления наблюдается для всех прозрачных кристаллов, за исключением принадлежащих к кубической системе. У так называемых одноосных кристаллов имеется направление, вдоль которого обыкновенный и необыкновенный лучи распространяются не разделяясь и с одинаковой скоростью. Это направление называется оптической осью кристалла. Следует иметь в виду, что оптическая ось – это не прямая линия, проходящая через какую-то точку кристалла, а определенное направление в кристалле. Любая прямая, параллельная данному направлению, является оптической осью кристалла.
Любая плоскость, проходящая через оптическую ось, называется главным сечением или главной плоскостью кристалла. Обычно пользуются главным сечением, проходящим через световой луч.
Оба луча, обыкновенный и необыкновенный, полностью поляризованы во взаимно перпендикулярных направлениях (см. рис.3.6). Плоскость колебаний обыкновенного луча перпендикулярна к главному сечению кристалла. В необыкновенном луче колебания вектора 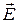 совершаются в плоскости, совпадающей с главным сечением.
совершаются в плоскости, совпадающей с главным сечением.
В некоторых кристаллах один из лучей поглощается сильнее другого. Это явление называется дихроизмом. Весьма сильным дихроизмом в видимых лучах обладает кристалл турмалина. В нем обыкновенный луч практически полностью поглощается на длине 1 мм.Таким же свойством обладает поляроид – целлулоидная пленка, в которую введено большое количество одинаково ориентированных кристалликов сульфата йодистого хинина (в этих кристаллах один из лучей поглощается на пути примерно в 0.1 мм). Следовательно, поляроид может быть использован в качестве поляризатора.
Двойное лучепреломление объясняется анизотропией кристаллов. В кристаллах некубической системы зависимость от направления обнаруживает, в частности, диэлектрическая проницаемость ε. В одноосных кристаллах ε в направлении оптической оси и в направлениях, перпендикулярных к ней, имеет различные значения 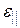 и
и 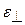 . В других направлениях ε имеет промежуточные значения.
. В других направлениях ε имеет промежуточные значения.
Поскольку
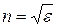 , (3.8)
, (3.8)
то из анизотропии ε вытекает, что электромагнитным волнам с различными направлениями колебаний вектора 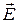 соответствуют разные значения показателя преломления п. Поэтому скорость световых волн в кристалле будет зависеть от направления колебаний светового вектора
соответствуют разные значения показателя преломления п. Поэтому скорость световых волн в кристалле будет зависеть от направления колебаний светового вектора 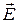 .
.
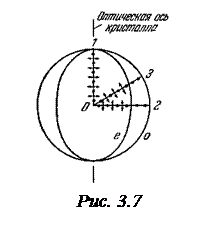 В обыкновенном луче колебания светового вектора происходят в направлении, перпендикулярном к главному сечению кристалла (на рис.3.7 эти колебания изображены точками на соответствующем луче). Поэтому при любом направлении обыкновенного луча (на рис.3.7 указаны три направления: 1, 2 и 3) вектор
В обыкновенном луче колебания светового вектора происходят в направлении, перпендикулярном к главному сечению кристалла (на рис.3.7 эти колебания изображены точками на соответствующем луче). Поэтому при любом направлении обыкновенного луча (на рис.3.7 указаны три направления: 1, 2 и 3) вектор 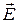 образует с оптической осью кристалла прямой угол и скорость световой волны будет одна и та же, равная
образует с оптической осью кристалла прямой угол и скорость световой волны будет одна и та же, равная
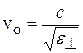 . (3.9)
. (3.9)
Изображая скорость обыкновенного луча в виде отрезков, отложенных по разным направлениям, мы получим сферическую поверхность. На рис.3.7 показано пересечение этой поверхности с плоскостью чертежа. Представим себе, что в точке О кристалла помещается точечный источник света. Тогда построенная нами сфера будет не что иное, как волновая поверхность обыкновенных лучей в кристалле. Колебания в необыкновенном луче совершаются в главном сечении. Поэтому для разных лучей направления колебаний вектора 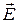 (на рис.3.7 эти направления изображены двусторонними стрелками) образуют с оптической осью разные углы. Для луча 1 угол равен π/2, вследствие чего скорость равна
(на рис.3.7 эти направления изображены двусторонними стрелками) образуют с оптической осью разные углы. Для луча 1 угол равен π/2, вследствие чего скорость равна 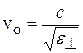 ; для луча 2угол равен нулю, и скорость равна
; для луча 2угол равен нулю, и скорость равна 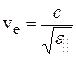 . Для луча 3 скорость имеет промежуточное значение. Таким образом, волновая поверхность необыкновенных лучей представляет собой эллипсоид вращения. В местах пересечения с оптической осью кристалла сфера и эллипсоид соприкасаются.
. Для луча 3 скорость имеет промежуточное значение. Таким образом, волновая поверхность необыкновенных лучей представляет собой эллипсоид вращения. В местах пересечения с оптической осью кристалла сфера и эллипсоид соприкасаются.
В зависимости от того, какая из скоростей, vо или ve, больше, различают положительные и отрицательные одноосные кристаллы. У положительных кристаллов ve<v0 (nе>n0). У отрицательных кристаллов ve> v0 (ne<n0).
Искусственное двулучепреломление. Двойное лучепреломление может возникать в прозрачных изотропных телах, а также в кристаллах кубической системы под влиянием различных воздействий: сильного однородного электрического (эффект Керра) или магнитного поля, а также при механических деформациях тел. Мерой возникающей оптической анизотропии может служить разность показателей преломления обыкновенного и необыкновенного лучей. Опыт показывает, что эта разность пропорциональна механическому напряжению σ в данной точке тела (то есть силе, приходящейся на единицу площади):
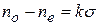 , (3.10)
, (3.10)
где k – коэффициент пропорциональности, зависящий от свойств вещества.
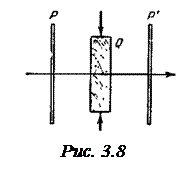 Поместим стеклянную пластинку Q между скрещенными поляризаторами Р и Р' (рис.3.8). Пока стекло не деформировано, такая система свет не пропускает. Если же стекло подвергнуть деформации (например, одностороннему сжатию), свет через систему начинает проходить, причем наблюдаемая в прошедших лучах картина будет испещрена цветными полосами. Каждая такая полоса соответствует одинаково деформированным местам пластинки. Следовательно, по характеру расположения полос можно судить о распределении напряжений внутри пластинки.
Поместим стеклянную пластинку Q между скрещенными поляризаторами Р и Р' (рис.3.8). Пока стекло не деформировано, такая система свет не пропускает. Если же стекло подвергнуть деформации (например, одностороннему сжатию), свет через систему начинает проходить, причем наблюдаемая в прошедших лучах картина будет испещрена цветными полосами. Каждая такая полоса соответствует одинаково деформированным местам пластинки. Следовательно, по характеру расположения полос можно судить о распределении напряжений внутри пластинки.
На искусственном двойном лучепреломлении основывается оптический метод исследования напряжений. Изготовленная из прозрачного изотропного материала (например, из целлулоида или плексигласа) модель какой-либо детали или конструкции помещается между скрещенными поляризаторами. Модель подвергается действию нагрузок, аналогичных тем, какие будет испытывать само изделие. Наблюдаемая при этом в проходящем белом свете картина позволяет определить распределение напряжений, а также судить об их величине.
Дата добавления: 2015-09-07; просмотров: 2409;
