Термодинамиканың екінші бастамасы.

Термодинамиканың бірінші бастамасы негізінде қандай да бір жылу көзінен алынған жылудың Q мөлшерінің есебінен жұмыстық зат (газ) А жұмысын атқарып отырады.

Пайдалы әсер коэффициенті 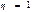болатын жылу қозғалтқыштары төтенше тиімді қозғалтқыш болған болар еді. Өйткені мұндай қозғалтқыш жасау үшін қыздырғыш пен суытқыштың болуы шарт емес. Ондай қозғалтқыштар қоршаған ортадағы кез келген денені, мысалы жер қыртысыны немесе мұхитты, айналадағы ең суық денелер температураларына тең температураларға бейін суыту есебінен жұмыс жасай алатын болар еді. Мұндай қозғалтқыш екінші ретті (текті) перпетуум мобильді энергияның сақталу заңына қайшы келеді.

Карно циклі бойынша жұмыс жасайтын жұмыс денесіне берілген 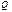жылуы толығымен жұмыс атқармайды. Суытқыш температурасы абсолют нольден жоғары ( 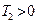) болса, қыздырғыштың жылуы суытқышқа берілмей қоймайды.

Кейінерек термодинамиканың екінші бастамасына Клаузиус, Томсон, Планк анықтамалар берді.

Бұл келтірілген анықтамалардың барлығы бір денеден нақты жылу мөлшерін алып, ол жылуды толығымен жұмысқа айналдыратын процесті іске асыруға мүмкін емес деген тұжырымға саяды.

Бұл принцип термодинамиканың екінші бастамасы деп атайды.

Жылу машиналарында жылудың жұмысқа айналуы міндетті түрде қосымша процеспен, яғни 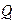жылу мөлшерін суығырақ денеге ауыстыру процесімен қатар жүреді, соның салдарынан ыстығырақ денеден алынатын 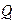жылу мөлшерін толығынан жұмысқа айналдыру мүмкін емес.

Карно циклінің пайдалы әсер коэффициенті үшін жазылған теңдеулеріне

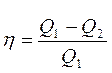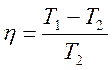, (27)

сүйене отырып

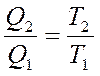немесе 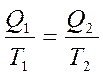(28)

деп жазуға болады. Сонда 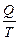-қатынасты келтірілген жылу мөлшері деп атайды. Карноның қайтымды циклында жылудың келтірілген мөлшерінің қосындысы нольге тең болады:

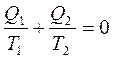(29)

Бірақ Карноның кез келген циклында п.ә.к. мынадай теңсіздікті қанағаттандырады:

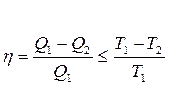(30)

мұндағы «=» таңбасы қайтымды процесс үшін орындалады.

Сондықтан Карноның кез келген циклында жылудың келтірілен мөлшерінің қосындысы нөлден артық бола алмайды. Бұл теңсіздік 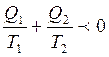Клаузиус теңсіздігі деп аталады.

Көпшілік жағдайда келтірілген жылу мөлшерін процестің белгілі бір бөлігінде нақты есептеу мақсатында оны элементар бөліктерге (5-*сурет) бөледі. Элементар цикл үшін Клаузиус теңсіздігі:

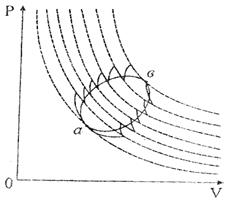
5-сурет

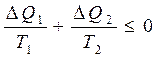(31)

Сонда жалпы толық цикл үшін бұл теңсіздікті:

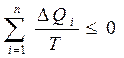(32)

Бұл қосынды шекті жағдайда тұйық контур бойынша алынған интегралға тең:

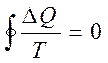(33)

Кез келген қайтымды тұйық емес процесте 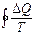шамасының процесс жүріп өткен жолға тәуелді болмайтындығын көрсетеді. Ол жүйенің бастапқы және соңғы күйлеріне ғана тәуелді. Бұдан дененің жүйенің күйімен сипаттамасы қандай да бір S шамасы болады. Сондықтан жүйенің А күйін сипаттайтын шаманы S_A деп, ал В күйіне сәйкес келетін шамасын S_B деп белгілейік, қайтымды процесте S_B-S_A айырымы

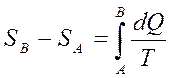(34)

Яғни бұл айырым А және В күйлердің арасында өтетін қайтымды процесте жылудың келтірілген мөлшерінің қосындысына тең болады.

Қорытындысында қайтымды процесс үшін элементар жылудың келтірілген мөлшері 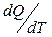жүйенің S функциясының толық дифференциалы болып табылады. Бұл S функциясы 1866 жылы Р.Клаузиус енгізіп, оны энтропия деп атады.

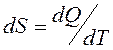(35)

немесе 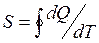(36)

Осы (36) теңдеуге сәйкес ішкі энергия мен энтропия өзгерісін қайтымды процесс үшін мынадай түрде жазуға болады:

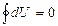(37)

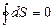(38)

Сонымен ішкі энергия сияқты энтропияда P, V, T параметрлерінің функциясы болып табылады:

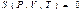(39)

Ал кез келген изопроцестер үшін (39) теңдеуді

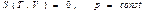(изобаралық процесс)

(изохоралық процесс)

(изотермиялық процесс)

Энтропия тұрақты жағдайда өтетін процессті изоэнтропиялық процесс деп атайды. Оған адиабаталық процесті жатқызуға болады. Жоғарыдағы (39) өрнектен

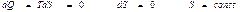(40)

Жоғарыда жазылған (39) және (40) теңдеулерге сүйене отырып, әр түрлі изопроцестерге сәйкесті энтропияны есептеуге болады.

Идеал газ үшін 1 күйден 2 күйге өткен кездегі оның энтропия өзгерісі

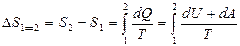(41)

мұндағы , , .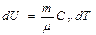

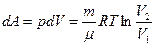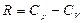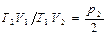еске алсақ, онда

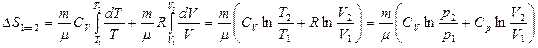(42)

Идеал газда өтетін процестер кезіндегі энтропия өзгерісі

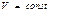
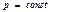
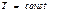
Изохоралық	Изобаралық	Изотермиялық	Адиабаталық

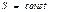
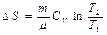
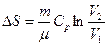
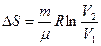
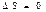
Энтропия:

1) Өз еркімен жүретін қайтымды процестерде тұйық жүйенің энтропиясы тұрақты күйінде қалады.

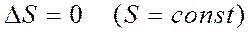
2) Қайтымды процесc кезінде процеске қатысатын денелердің өзгерістерінің алгебралық қосындысы нольге тең болады:

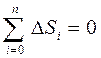
3) Қайталанбайтын процестерде тұйық жүйенің энтропиясы міндетті түрде өседі:

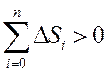
Бұл теңсіздік қайтымды процеске қатысушы барлық денелердің энтропиялары өзгерістерінің алгебралық қосындысы әрқашанда нольден үлкен болады. Клаузиус енгізген бұл теңсіздік энтропияның өсу принципі деп аталады.

Бұл жерде жүйеге енетін денелердің энтропиялары бірдей өседі деген ой тумауы керек. Өйткені жүйеге бірігетін денелердің энтропиясы азайса, ал екіншісінікінің өсуімен жойылып отырады да, жалпы процес кезінде энтропия өсуі байқалады. Мысалы газды изотермиялық жағдайда сыққанда, оның энтропиясы азаяды. Бірақ термостаттың энтропиясы өседі (термостат жылу алады).

Сонымен қайтымды және қайтымсыз процестер үшін термодинамиканың екінші бастамасы:

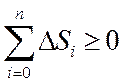
Табиғатта кездесетін процестер қайтымсыз процестер болатындықтан, оқшауланған жүйелерде энтропияның өсуіне әкелетін процестер жүреді.

Термодинамикалық потенциалдар.

Термодинамикадлық есептерде термодинамикалық потенциалдар деп аталатын күй функцияларын пайдалануға болады. Тәуелсіз параметрлердің әрбір жиынтықтарына термодинамикалық потенциалдар сәйкес келеді.

Термодинамикалық потенциалды қарастырған кезде

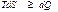(43)

қатынасын пайдаланады. Мұндағы теңдік белгісі ( 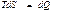) қайтымды, ал теңсіздік 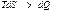қайтымсыз процестерге жатады.

Ішкі энергия. Термодинамиканың бірінші бастамасын қайтымды процесс үшін

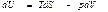(44)

деп жазуға болады. Мұнда U потенциалы үшін айнымалылар S және V болып табылады. Олай болса,

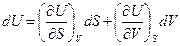(45)

Осы (45) өрнекті (44) теңдеумен салыстырсақ, онда

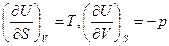(46)

Адиабаталық процесс үшін сыртқы күштерге қарсы атқарылатын жұмыс

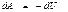
немесе

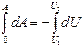
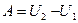(47)

Сонда тұрақты көлемдегі жылусыйымдылық

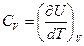(48)

Еркін энергия. Жоғарыдағы (44) теңдеу түрінде жазылған термодинамиканың бірінші бастамасындағы атқарылған жұмысты

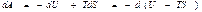(49)

деп жазуға болады. Сонда еркін энергия

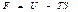(50)

дененің күй функциясы деп атайды.

Сонда (49), (50) теңдеулерге сәйкес қайтымды изотермиялық процесс кезінде атқарылатын жұмыс дененің еркін энергиясының өзнерісіне тең болады:

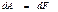(51)

немесе

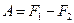(52)

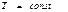( қайтымды)

Енді (47) теңдеумен (52) теңдеуді салыстырсақ, изотермиялық процесс кезінде ішкі энергия еркін энергияның адиабаталық процесс кезінде тәрізді роль атқаратынын көреміз.

Қарастырған (47) теңдеу қайтымды және қайтымсыз процестер үшін оырндалады. Ал (10) теңдеу тек қайтымды процесс үшін орындалады.

Қайтымсыз процесс үшін еркін энергия

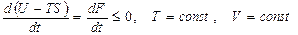(53)

мұндағы: t - уақыт. Бұл (53) теңдеуден ( 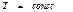) тұрақты температура мен 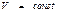тұрақты көлемде өтетін процестерде процесс еркін энергияның төмендеуі есебінен іске асырылады. Жүйе тепе-теңдікке келген уақытта F өзінің уақыт бойынша өзгертуін тоқтатады. Яғни T мен V шамалары тұрақты болған кезде тепе-теңдік күй еркін энергияның аз мәніне сәйкес келетін күй болып табылады.

Энтальпия. Егер процесс тұрақты қысымда өтетін болса, онда дененің алатын жылуын

(54)

H=U+pV (55)

Н- күй функциясын энтальпия немесе жылу функциясы деп атайды.

Сонда (49) және (55) теңдеулер дененің изобаралық процесс кезінде алатын жылу мөлшерін

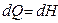(56)

немесе интегралдық түрде

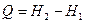(57)

болатындығын көреміз. Демек, қысым тұрақты болған кезде дененің алатын жылуы энтальпияның өсімшесіне тең болады.

Тұрақты қысым кезіндегі энтальпия тұрақты көлем кезіндегі ішкі энергия ролін атқарады.

Негізгі әдебиеттер:

1. Әлжанов К.К., Құсаинов К.К., Мүсенов К.Қ., Дәрібеков С. Молекулалық физика. Қарағанды. ҚарМУ.2003

2. Құлбекұлы М. Молекулалық физика және термодинамика. Алматы, Қарасай баспасы. 2005

3. Қойшыбаев Н. Молекулалық физика. Алматы, Зият пресс баспасы. 2005

Қосымша әдебиеттер:

1. Қойшыбаев Н., Шарықбаев А.О. Физика. Алматы. 2001

2. Савельев И.В. Жалпы физика курсы. М., Наука, 1986.

3. Дәрібеков С. Материалдар физикасының негіздері. ҚарМУ 2005.