Тербелістер мен толқындар

Кез келген физикалық жүйеде тербелмелі қозғалыс пайда болу үшін оған сырттан энергия беру керек. Мысалы, математикалық маятникті тепе-теңдік күйінен ауытқыту арқылы оның потенциал энергиясын арттыру керек. Тербеліс кезінде потенциал энергия кинетикалық энергияға, кинетикалық энергия потенциал энергияға алма-кезек айналып жүйеде тербеліс пайда болады. Егер айналыстағы энергия жылуға айналып ысырап болмаса, тербелмелі қозғалыс шексіз жүреді, яғни тербеліс гармоникалық болады. Тербелістегі энергия ысырап болмайтын жүйені мүлтіксіз (идеальный) жүйе деп атайды.

Егер тербелістегі энергия жылу энергиясына айналып ысырап болмаса электрмагнит тербеліс шексіз ұзаққа созылып тербеліс гармоникалық болады.

Бұл баяндалған деректерден мынадай қорытындылар жасауға болады:

- тербеліс пайда болу үшін жүйені тепе-теңдік күйден шығару үшін оған сырттан энергия беру керек;

- тізбекке берілген энергия бір түрден екінші түрге алма-кезек айналып жүйеде тербеліс пайда болады;

- егер тербеліс кезінде айналыстағы энергия жылу энергиясына айналып ысырап болмаса, тербелмелі қозғалыс шексіз ұзақ созылып тербеліс гармоникалық тербеліске айналады.

Тербелістің кез келген ортада таралуын толқын деп атайды. Оларға: дыбыс толқындары, сағат механизмнің жұмысы, тізбектегі айнымалы ток, электромагниттік тербелістер және т.б. жатады.

Жалпы физика курсында көбінесе тек бірдей қайталанып отыратын процестерді қарастырып, оның негізгі кинематикалық теңдеулерін жазатын боламыз.

Периодтық қозғалыс деп әрбір циклі дәлме-дәл кез келген басқа циклін қайталап отыратын қозғалысты атайды. Бір цикл ұзақтығын период деп атайды.

Тербелмелі қозғалысты ерікті және еріксіз деп екіге бөледі. Ерікті қозғалыста сыртқы күштің әсерінсіз өз бетінше қозғалыс циклін қайталап отырады. Мұндай тербелістерді еркін тербелістер деп атайды.

Өз бетінше периодтық қозғалыстар жасай алатын немесе тербелетін осы тәрізді денелер немесе денелер жүйесін (материалдық нүктелер жиынтығын) тербелмелі жүйелер деп атаймыз.

Тербелістерді зерттеуді біз механикалық жүйелердің ең қарапайым түрлері: математикалық маятник, физикалық маятник, серпелі маятник, тербелмелі контурды қарастырамыз.

Математикалық маятник және оның кинематикасы.

Математикалық маятник деп – ауырлық центрі іліну нүктесінен төмен болатындай етіп ілінген кез келген денені айтады.

Еркін тербелістерді жасай алатын кез келген системаның орнықты тепе-теңдіік қалпы болады. Математикалық маятник үшін бұл қалып оның ауырлық центрі мен іліну нүктесі вертикалдық бойында және ауырлық центрі іліну нүктесінен төмен орналасатын жағдайға сәйкес келеді.

Егер біз маятникті тепе-теңдік қалпынан шығаратын болсақ, онда тепе-теңдік қалпының оң жағына, бір сол жағына шығып, тербеле бастайды. Маятниктің тепе-теңдіктен ең үлкен ауытқуын тербелістің амплитудасы деп атайды. Амплитудданың бастапқы қозғалыс шартына тәуелділік қасиеті барлық тербелмелі қозғалыстарға тән деуге болады.

Тербелмелі қозғалыстың периодтылығын (ырғақтылығын) сипаттайтын Т шамасын тербелістің периоды деп атайды. Тербелістің периодын толық бір тербеліске кеткен уақытпен өлшейді.

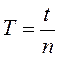(1)

мұндағы: n- тербеліс саны, t- сол n тербеліске кеткен уақыт.

Тербелмелі қозғалыстың қайталанғыштық жылдамдығын сипаттайтын шаманы оның 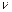жиілігі деп атайды.

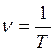(2)

Дене тербелісінің жиілігін бірлік уақыттағы толық тербелістер санымен өлшейді.

Ал 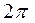секунд ішінде жасалатын тербеліс санын циклдік (дөңгелек) жиілік ( 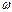, Гц) деп атайды.

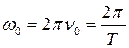(3)

Әрбір уақыт мезетіндегі тербелістегі нүктенің координата фазасымен ( 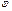, рад, градус) сипатталады.

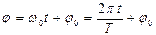(4)

Мұндағы 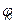- бастапқы фаза, яғни 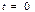мезеттегі фазаның мәні.

Тепе-теңдіктен ауытқытылған математикалық маятникке, жіптің керілу күші – Т, ауырлық күші P=mg және қалпына келтіруші күш F және жіптің реакция күші N әсер етеді. (2-cурет)

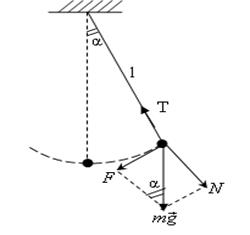
2-сурет

Қалпына келтіруші күштің моменті

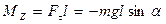(5)

мұндағы 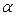- маятниктің тепе-теңдіктен ауытқушы бұрышы, 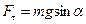- қалпына келтіруші күш, l –маятник жібінің ұзындығы, g – еркін түсу үдеуі, 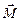мен 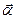ауытқу (псевекторлар) векторларының бағыттары бір-біріне қарама-қарсы болғандықтан (5) теңдеуінің алдына «-» таңбасы қойылады.

Қатты дененің динамикасының 2-ші заңы бойынша

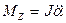(6)

мұндағы J- маятниктің инерция моменті. Енді (5), (6) теңдеулерінен

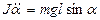(7)

Маятниктің тепе-теңдіктен аз ауытқыған жағдайы үшін 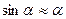және 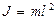тең екендігін ескере отырып (7) теңдеуді

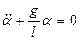(8)

мұндағы 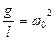деп белгілеп

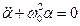(9)

жазып, бұл теңдеуді тербелістің дифференциалдық теңдеуімен салыстырсақ, онда математикалық маятниктің гармоникалық тербелісінің

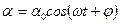(10)

гармоникалық заңы түрінде жазуға болады.

Сонда

,

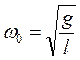ал периоды

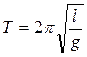(11)

Бұл теңдеу математикалық маятник үшін жазылған Томсон формуласы деп атайды.

Физикалық маятник. Қатты дене (3-сурет ) ауырлық күшінің әсерінен горизонталь бағытта С масса центрімен сәйкес келмейтін О нүктесінің маңында тербелмелі қозғалысқа түседі. О нүктесін ілу нүктесі деп атайды. Қалпына келтіруші күштің моменті:

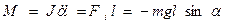
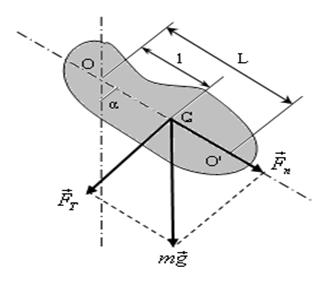
3-cурет

мұндағы J - ілу нүктесі арқылы өтетін оське қатысты инерция моменті, 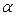- маятниктен тепе-теңдіктен ауытқу бұрышы, 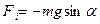- қалпына келтіруші күш, l=OC маятниктің масса центрі мен ілу нүктесінің аралығы.

Динамиканың екінші заңы бойынша қалпына келтіруші күш үшін

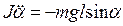
сонда 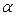-аз мәні үшін

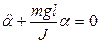
физикалық маятник гармоникалық тербеліс жасайды.

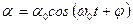
мұндағы: 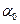- тербелістің циклдік (дөңгелек) жиілігінің амплитудасы

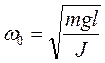
периоды

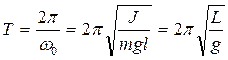(12)

мұндағы: 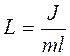- физикалық маятниктің келтірілген ұзындығы деп аталады.

ОС түзуінің бойында жатқан О ілу нүктесінен келтірілген ұзындыққа L тең аралықта жатқан О' нүктесін физикалық маятниктің тербелу центрі деп атайды. Физикалық маятниктің ілу нүктесі мен тербеліс центрілерін өзара алмастыруға болады. Бұл жағдайда физикалық маятниктің тербеліс периоды өзгермейді.

Жоғарыдағы (12) теңдеуді физикалық маятник үшін Томсон формуласы деп атайды.

Серіппелі маятник – абсолютті серпімді серіппеге ілінген массасы m жүйе серпімді күштің әсерінен түзу сызықты гармоникалық қозғалыс жасайды (4-сурет)

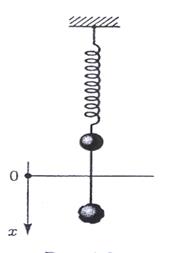
4-сурет

Маятникті қалпына келтіруші күші деформацияланған серіппенің ығысу шамасы тура пропорционал болады.

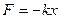
мұндағы: k- серіппенің қатаңдығы.

Маятниктің қозғалыс теңдеуі

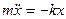
дифференциалдық теңдеуі

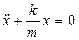немесе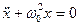

Серпімді күштің әсерінен ол вертикаль тік бағытта гармоникалық тербеліс жасайды.

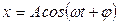
циклдік (дөңгелек) жиілігі

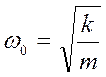
периоды

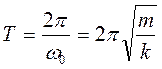(13)

Бұл (10) теңдеуді серіппелі маятник үшін Томсон формуласы деп атайды.

Тербелістегі нүктенің берілген уақыт мезетіндегі тепе-теңдік қалпына қатысты орын сипаттайтын шаманы ығысу деп атайды.

Ығысуды тербелістегі нүктенің орнықты тепе-теңдік қалпынан оның осы уақыт мезетіндегі орнына дейінгі қашықтықпен өлшейді.

А – амплитуда сан мәні жағынан тербелістегі нүктенің орнықты тепе-теңдік қалпынан ең үлкен 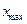ауытқуына тең шама

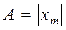
Гармоникалық тербелістің теңдеуі, жылдамдығы, үдеуі және энергиясы мен сызбасы (графигі).

Тербелмелі нүктенің ығысуының уақытқа тәуелділігін өрнектейтін формуланы тербелмелі қозғалыстың теңдеуі деп атайды. Ол гармоникалық тербеліс теңдеуімен сипатталады.

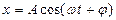(14)

Механикалық гармоникалық тербелістені нүктенің жылдамдығы, үдеуі, энергиясы

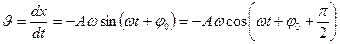(15)

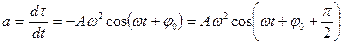(16)

мұндағы 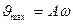, 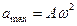-жылдамдық пен үдеу амплитудалары.

Бұл (15), (16) теңдеулерден тербелмелі қозғалыстың жылдамдығы мен үдеуі, жиілігі х ығысу жиілігіндей болатын гармоникалық заңдылық бойынша жүреді. Жылдамдық (14) фазасы, үдеу (15) фазасынан сәйкесті ығысу фазасын 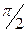және 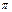айырылады (5 – сурет).

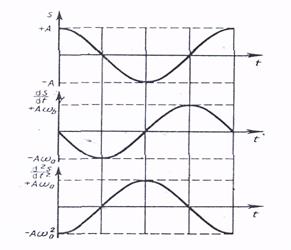
5-сурет

Материалдық нүктенің гармоникалық тербелісінің кинетикалық энергиясы

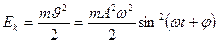(17)

немесе

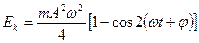(18)

Серпімді 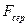күштің әсерінен гармоникалық тербеліс жасайтын материалдық нүктенің потенциалдық энергиясы

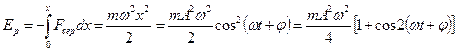(19)

Толық энергия

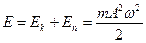(20)

Бұл (18) және (19) теңдеулерден кинематикалық энергия мен потенциалдық энергиялардың жиілігі ( 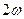), яғни гармоникалық тербеліс жиілігінен екі есе көп болады (6-сурет). Өйткені 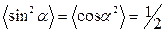, онда (17) және (19) теңдеулерінен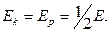

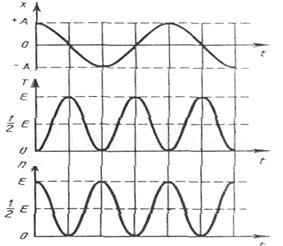
6-сурет

Гармоникалық тербелістерді қосу.

1. Бағыттары мен жиіліктері бірдей гармоникалық тербелістерді қосу.

Тербелетін денеде бірнеше тербелмелі процестер жүруі мүмкін. Сондықтан осындай тербелістердің қорытқы амплитудасын анықтау керек болады.

Жиіліктері мен бағыттары бірдей гармоникалық тербелістерді қосу үшін векторлық диаграмма әдісін қолданады (7-сурет).

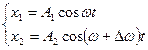
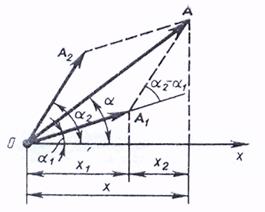
7-сурет

Қорытқы ығысу амплитудасы мен бастапқы фазасы

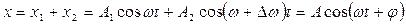(21)

мұндағы

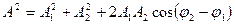(22)

Бастапқы фаза

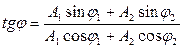(23)

Қорытқы гармоникалық тербелістің амплитудасы фаза айырымына 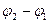тәуелді болады.

Енді (22), (23) теңдеулерді талдайтын болсақ, онда

1)

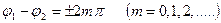
Қорытқы тербелістің амплитудасы жеке тербелістердің амплитудаларының алгебралық қосындысына тең болады:

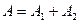
2)

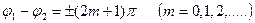
Қорытқы тербелістің амплитудасы жеке тербелістер амплитудасның айырымына тең

.

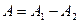Бір бағытта тербелетін қосылатын екі тербелістің жиіліктері бір-бірінен сәл өзгешелеу 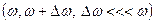. Қорытқы тербелістің амплитудасы периодты түрде өзгереді, мұндай тербелісті соғу деп атайды.

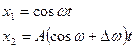
Сонда

()

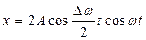Мұндағы 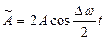соғу амплитудасы деп, ал 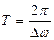соғу периоды деп атайды.

Өшетін тербелістер.

Реал (нақты) тербеліс жүйесінде кедергі күші 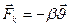әсерінен нүктенің энергиясы imкi энергияга айналады, соның салдарынан уақыт өтуімен бipre оның тербеліс амплитудасы азаяды. Мұндай козғалыс мына дифференциалдық теңдеумен сипатталады:

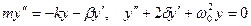
мұндағы 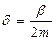- өшу коэффициенті, 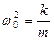- ортаның кедергісі болмағанда ( 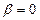) жүйенің жасайтын еркін тербелістерінің жиілігі.

Тербеліс теңдеуі:

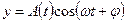
мұндағы: 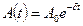- өшетін тербелістің амплитуда­сы, А_о— бастапкы амплитуда.

Бip-бipiнен периодқа сәйкес уакытқа ажыратылатын амплитудалар катынасының логарифмі логарифмдік декремент деп аталады:

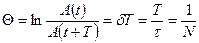
Амплитуда е ~2,7 есе кемитін 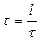(релаксация уақыты) уақыт ішінде жүйе 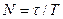тербеліс жасап үлгереді. Тербелмелі жүйені сипаттау үшін сапалық (Q) деп аталатын шама енгізеді:

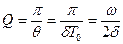
Өшетін тербелістің периоды мен жиілігі мынаған тең:

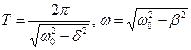
Орта кедергісі аз болған жағдайда, яғни .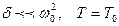

Еріксіз тербелістер деп тербелмелі жүйеде периодты түрде өзгеретін 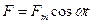күштің әсерінен пайда болатын өшпейтін тербелістерді айтады.

Серіппелік маятниктің қозғалысының дифференциалдық теңдеуі былай жазылады:

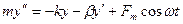
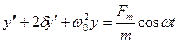
мұндағы: 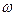-сыртқы әсер ететін күш жиілігі. дифференциалдық теңдеулер теориясынан біртекті емес теңдеудің жалпы шешімі оған сәйкес келетін біртекті теңдеудің жалпы шешімі мен біртекті емес теңдеудің 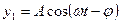дербес шешімінің қосындысына тең.

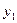( ) қосылғышы тербелістің орнығуы деп атайды, ол бастапқы кезеңде ғана роль атқарып, уақыт өткен сайын кемиді, оны ескермеуге де болады.

Сонымен (y) функциясы орныққан еріксіз тербелістерді сипаттайды:

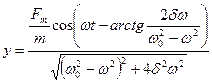
Еріксіз тербелістің амплитудасы мәжбүр теуші күштің 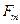амплитудасына пропорционал және оның жиілігіне тәуелді:

.

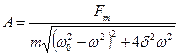Еріксіз тербелістер фазасы бойынша мәжбүр теуші күштен қалып қояды да, әрі қалу шамасы мәжбүр етуші күш жиілігі 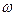-ға тәуелді.

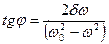
Сыртқы күштің 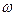жиілігі жүйенің меншікті 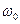жиілігіне жақындағанда еріксіз тербеліс амплитудасының ең үлкен мәніне жету құбылысы резонанс деп, ал оған сәйкес келетін жиілік резонанстық жиілік деп аталады.

Механикалық толқындар. Серпімді ортада тербелістің таралуын механикалық толқын деп атайды. Орта бөлшектерінің тербеліс бағыты толқынның таралу бағытымен бағыттас болса, онда толқындарды қума, ал толқынның таралу бағытына перпендикуляр бағытталған болса, көлденең толқындар деп атайды.

Толқын фронты (немесе толқындық бет ) деп, бірдей фазаларда тербелетін нүктелердің геометриялық орнын айтамыз. ТОлқын фронтының түріне байланысты толқындар жазық және сфералық болып бөлінеді.

Бірдей фазада тербеліп тұрған екі жақын жатқан нүктенің ара-қашықтығын толқын ұзындығы деп атайды:

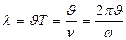
мұндағы: Т – тербеліс периоды, 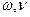-жиілік.

Толқын теңдеуін және оның шешімін мына түрде жазуға болады:

, ,

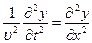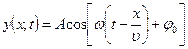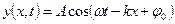
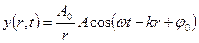
мұндағы: х – О толқындық көзінен ортаның қарастырып жатқан А нүктесіне дейінгі арақашықтық, 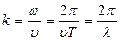- толқындық сан, ол 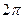– ұзындық бірлігіне қанша толқын жайғасатынын көрсететін сан.

Толқын фазасы тұрақты десек, яғни 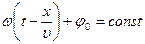, онда фазалық жылдамдық , яғни фазаның орын ауыстыру жылдамдығы:

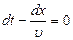, бұдан .

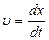(1) өрнегі х шамасының арту бағытында таралатын жазықтық, ал (2) сфералық толқынның теңдеуінде r – толқын көзінен ортаның қарастырып отырған нүктесіне дейінгі ара-қашықтық, ал А – толқын көзінен 1-ге тең қашығы сан жағынан амплитудаға тең тұрақты шама. Қума және көлденең толқындардың фазалық жылдамдықтары мынаған тең:

,

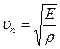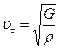
мұндағы: E, G – Юнг, ығысу модульдері, 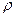-ортаның тығыздығы.

Негізгі әдебиеттер:

1. Абдула Ж., Т. Аязбаев. Физика курсының лекциялары. Дәуір, 2012

2. Ақылбаев Ж.С., Гладков В.Е., Ильина Л.Ф., Турмухамбетов А.Ж., Механика. Астана, Фалиант баспасы, 2004.

3. Қойшыбаев Н., Шарықбаев А.О. Физика. Алматы, 2001

Қосымша әдебиеттер:

1. Қойшыбаев Н. Механика. Алматы, Зият пресс баспасы, 2005

2. Савельев И.В. Жалпы физика курсы. М., Наука, 1986.