Лабораторная работа 3. Построение графинов функций и поверхностей.
Цель:
- Овладеть умениями построения графиков функций.
- Отработать алгоритм построения график поверхности.
Задание:
1. Построить график функций, заданной в декартовой системе координат.
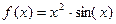
1. Задать функцию, используя знак присваивания.
2. Определить вид графика.
3. Вдоль оси ОХ ввести имя переменной х.
4. Вдоль оси OY ввести имя функций f(x).
5. Щелкнуть вне области поля построения графика.


2. Построить график функции, заданной параметрически.
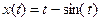
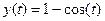
1. Задать функцию, используя знак присваивания.
2. Определить вид графика .
3. Вдоль оси ОХ ввести x(t)/
4. Вдоль оси OY ввести y(t).
5. Щелкнуть вне области поля построения графика.

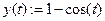

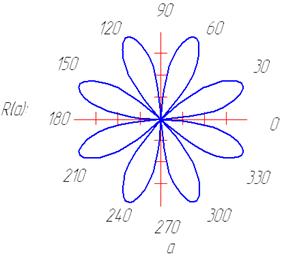
3. Построить график функции, заданной в полярной системе координат.

1. Задать функцию, используя знак присваивания.
2. Определить вид графика.
3. Вдоль оси ОХ ввести имя переменной а.
4. Вдоль оси OY ввести имя функции R(a).
5. Щелкнуть вне области поля построения графика.

4. Построить график функции от двух переменных.

1. Зададим интервал изменения для переменных х и y и шаг изменения.
Например 


 .
.
2. Определим функцию, используя знак присваивания.
3. Определим количество узлов и присвоим это значение переменной N.
4. Определим диапазон изменения индексов i и j по переменным х и y соответственно.
5. Подсчитаем значения переменных в узлах сетки.
6. Подсчитаем значения функции в узлах сетки.
7. Определить вид графика.
8. Ввести имя функции.
9. Щелкнуть вне области поля построения графика.
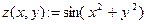
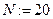

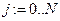

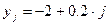


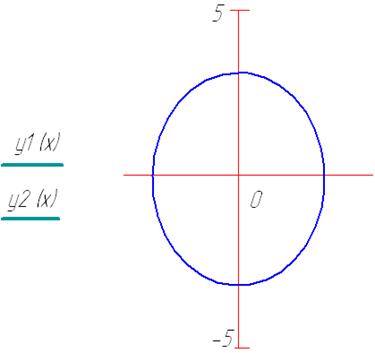
5. Построить график кривой второго порядка (эллипса).
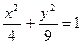
1. Разрешить уравнение относительно переменной y. (в выражении 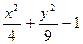 выделить у и выполнить команду Symbolics/Variable/Solve).
выделить у и выполнить команду Symbolics/Variable/Solve).
2. Определить две функции, согласно полученному решению, для верхней и нижней частей эллипса.
3. Определить вид графика.
4. Вдоль оси ОХ ввести имя переменной х.
5. Вдоль оси ОY ввести имена двух функций через запятую.
6. Щелкнуть вне области поля построения графика.
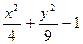

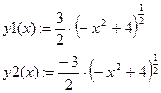
6. Выполнить задание согласно своему варианту.
6.1 Построить график функции, заданной в декартовой системе координат.
1.  6.
6. 
2. 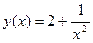 7.
7. 
3. 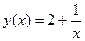 8.
8. 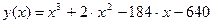
4. 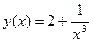 9.
9. 
5. 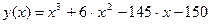 10.
10. 
6.2 Построить график функции, заданной параметрически.
1. 
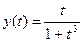 6.
6. 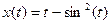
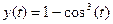
2. 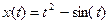
 7.
7. 
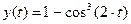
3. 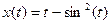
 8.
8. 
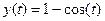
4. 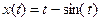
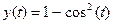 9.
9. 

5. 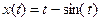
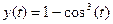 10.
10. 

6.3 Построить график функции, заданной в полярной системе координат.
1.  6.
6. 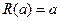
2.  7.
7. 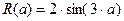
3. 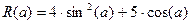 8.
8. 
4. 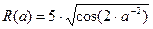 9.
9. 
5.  10.
10. 
6.4 Построить график функции от двух переменных.
1. 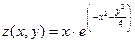 6.
6. 
2. 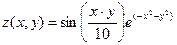 7.
7. 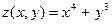
3. 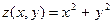 8.
8. 
4.  9.
9. 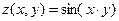
5. 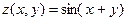 10.
10. 
6.5 Построить график кривой второго порядка (эллипса).
1. 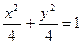 6.
6. 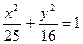
2. 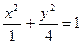 7.
7. 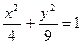
3.  8.
8. 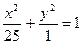
4. 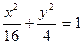 9.
9. 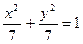
5. 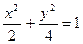 10.
10. 
Лабораторная работа 4. Графическое решение задач.
Цель:
- Обобщить полученные знания построения графиков при графическом решении математических задач.
- Овладеть навыками применения функции «Trace» для определения координат точки на графике.
Задание:
1. Решить графически уравнение:  .
.
1. Задать функцию, используя знак присваивания.
2. Построить график функции.
3. Выделив график функции, выполнить команду Format/Graph/Trace
4. Установить курсор в точке пересечения графика функции с осью ОХ.
5. Скопировать значения Х и Y ниже графика.


координаты точек
 -2.74
-2.74  -1.02
-1.02 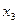 0.74
0.74
 -0.048024
-0.048024  0.05999
0.05999  0.048024
0.048024
Уравнение имеет три корня, значения которых приблизительно равны
 =-2.74
=-2.74  =-1.02
=-1.02 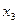 =0.74
=0.74
2. Найти графически максимальное и минимальное значения функции.
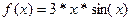 на интервале
на интервале  .
.
1. Задать функцию, используя знак присваивания.
2. Построить график функции. 
 .
.
3. Выделив график4 функции, выполнить команду Format/Graph/Trace…
4. Установить курсор в точке минимума функции и скопировать найденные значения в текстовый блок.
5. Установить курсор в точке максимума функции и скопировать найденные значения в текстовый блок.
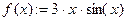

Точка минимума х=5.02 у=-14.353
Точка максимума х=8.02 у=23.729
3. Определить графически, сколько решений имеет система уравнений.
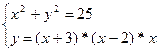
1. Построить графики функций.
2. Подсчитать количество точек пересечения графиков.
3. Записать ответ в текстовом блоке.

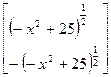
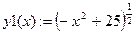

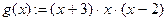
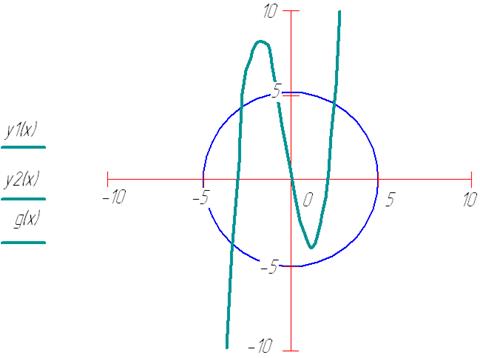
Ответ: Система имеет четыре решения, так как графики функций пересекаются в 4-х точках.
4. Подобрать переменные a,b,c и d так, чтобы система уравнений имела наибольшее число корней.
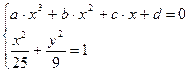
1. Графиком второго уравнения является эллипс, пересекающий ось ОХ в точках 5 и –5, поэтому корнями трехчлена возьмем числа из промежутка (-5;5).
2. Построить графики функций.
3. Задать значения х1, х2, х3 так, чтобы на графике было 6 точек пересечения.
4. Раскрыть скобки и привести подобные в выражении  .
.
5. Выписать коэффициенты a,b,c и d.

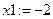

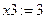

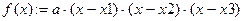
  
| уравнение для верхней части эллипса |
| уравнение для нижней части эллипса |
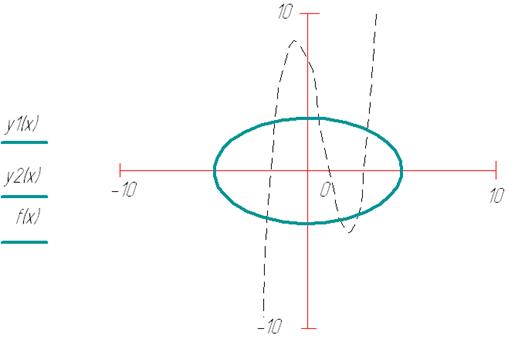
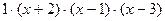
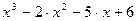
Ответ: а=1 b=-2 c=-5 d=6.
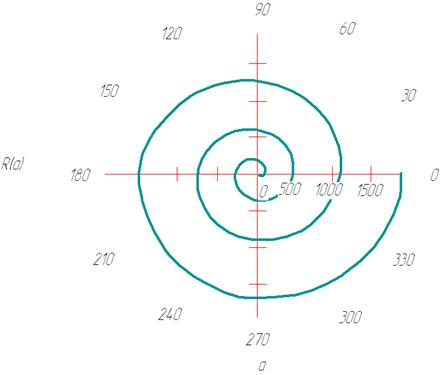
5. Применить эффект анимации к графику функции спираль Галилея  .
.
1. Ввести параметры изменения угла, а от 0 до 8*π с шагом 0,1.
2. Присвоить выражение для функции, дописывая к аргументу функцию FRAME.
3. Построить график функции в полярных координатах.
4. Выделив график функции, выполнить команду: View/Animate.
5. Через команду Options… установить программу сжатия «Полные кадры (без сжатия)».
6. Установить изменение функции FRAME от 0 до 100 с шагом 10.
7. Установив курсор в области графика, выполнить команду Animate.

6. Применить эффект анимации к графикам функций.
Лемниската Бернулли
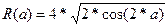
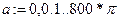
Кохлеоида

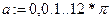
Улитка Паскаля

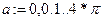
Роза

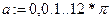
Контрольные вопросы:
1. С помощью, какой команды можно приблизительно определить координаты любой точки графика?
2. Что произойдет, если установить изменение функции FRAME от 100 до 0 с шагом 10?
3. Можно ли применять эффект анимации к графикам функций, построенных в декартовой системе координат? Проверьте.
Дата добавления: 2015-09-18; просмотров: 1478;
