Критерий согласияФишера

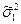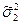Задача сравнения дисперсий сводится к проверке нулевой гипотезы Н₀, заключающейся в принадлежности двух выборок к одной и той же генеральной совокупности. Пусть необходимо сравнить две дисперсии и , полученные при обработке результатов моделирования и имеющие k₁ и k₂ степеней свободы соответственно, причем 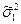> 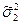. Для того чтобы опровергнуть нулевую гипотезу Н₀: 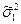= 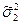необходимо при уровне значимости γ указать значимость расхождения между 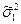и 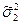. При условии независимости выборок, взятых из нор­мальных совокупностей, в качестве критерия значимости используется распределение Фишера (F-критерий) F= 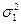/ 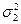, которое зависит только от числа степеней свободы k₁=N₁–1, k₂=N₂–1, где N₁ и N₂ – объемы выборок для оценк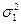и и 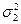соответственно.

Алгоритм применения критерия Фишера следующий: 1) вычисляется выборочное отношение F= 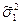/ 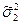; 2) определяется число степеней свободы k₁=N₁–1и k₂=N₂ –1; 3) при выбранном уровне значимости γ по таблицам F-распределения находятся значения границ критической области 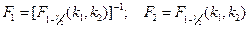; 4) проверяется неравенство F₁≤F≤F₂; если это неравенство выполняется, то с доверительной вероятностью β нулевая гипотеза Н₀: 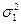= 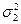может быть принята.

Хотя рассмотренные оценки искомых характеристик процесса функционирования системы, полученные в результате компьютерного эксперимента с моделью, являются простейшими, тем не менее, они охватывают большинство случаев, встречающихся в практике обработки результатов моделирования системы с целью ее исследования и проектирования.