Критерий согласияСмирнова

При оценке адекватности компьютерной модели реальной системе возникает необходимость проверки гипотезы Н₀, заключающейся в том, что две выборки принадлежат той же генеральной совокупности. Если выборки независимы и законы распределения совокупностей F(u) и F(z), из которых извлечены выборки, являются непрерывными функциями своих аргументов, то для проверки гипотезы Н₀ можно использовать критерий согласия Смирнова, при­менение которого сводится к следующему. По имеющимся результатам вычисляют эмпирические функции распределения F_э(u) и F_э(z) и определяют

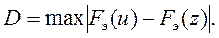
Затем при заданном уровне значимости γ находят допустимое отклонение

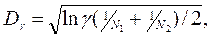
где N₁ и N₂ – объемы сравниваемых выборок для F_э(u) и F_э(z), и проводят сравнение значений D и D_γ: если D>D_γ, то нулевую гипотезу Н₀ о тождественности законов распределения F(u) и F(z) с доверительной вероятностью β=1– γ от­вергают.