Методы оценки
Методы оценки распределений и некоторых их моментов при достаточно большом объеме выборки, т.е. числе реализаций N, заключаются, прежде всего, в вычислении математического ожидания M[ξ]=μξ и дисперсии D[ξ]=σξ2 , т.е. соответственно первого и второго центральных моментов случайной величины ξ:
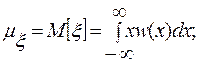
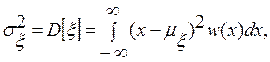
где w(x) – плотность распределения случайной величины ξ, принимающей значения x.
При проведении имитационного эксперимента со стохастической моделью системы определить эти моменты невозможно, как правило, из-за неизвестной априори (заранее) плотности распределения w(x). Поэтому при обработке результатов моделирования приходится довольствоваться лишь некоторыми оценками моментов, полученными на конечном числе реализаций N. При условии независимости наблюдений значений случайной величины ξ в качестве таких оценок используются:
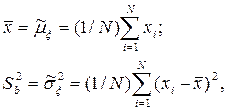
где 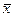 – выборочное среднее, а
– выборочное среднее, а 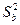 – выборочная дисперсия, которые используются в качестве оценок математического ожидания μξ и дисперсии σξ2соответственно.
– выборочная дисперсия, которые используются в качестве оценок математического ожидания μξ и дисперсии σξ2соответственно.
Оценки, полученные в итоге статистической обработки результатов моделирования, должны удовлетворять следующим требованиям.
1. Несмещенностьоценки означает равенство математического ожидания оценки определяемому параметру:
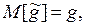
где 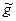 – оценка параметра g.
– оценка параметра g.
2. Эффективностьоценки означает минимальность среднего квадрата ошибки данной оценки: 
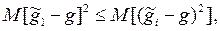
где 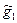 – рассматриваемая оценка;
– рассматриваемая оценка; 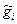 – любая другая оценка.
– любая другая оценка.
3. Состоятельностьоценки означает сходимость по вероятности при N→∞ к оцениваемому параметру:
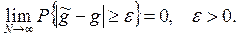
С учетом неравенства Чебышева достаточное условие выполнения этого неравенства заключается в том, чтобы
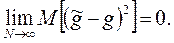
Дата добавления: 2015-09-18; просмотров: 577;
