Общие принципы построения блочных шифров

Симметричные системы шифрования информации подразделяются на блочные симметричные системы шифрования информации и поточные симметричные системы шифрования информации.

Блочная система шифрования информации есть система шифрования, в которой сообщение разбивается на информационные блоки фиксированной длины 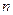бит и весь блок шифруется одновременно. Очень часто в литературе используется термин «блочный шифр», который является синонимом термина «блочная система шифрования информации».

В классе элементарных блочных шифров ограничимся рассмотрением наиболее универсальных и часто встречающихся шифров подстановки и перестановки.

В шифре подстановки каждый символ сообщения заменяется символом, определяемым функцией подстановки . Вид функции подстановки задается ключом .

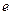Если функция подстановки 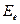фиксированная (ключ 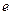является константой), то такой шифр называется простой заменой или одноалфавитной подстановкой. Такой шифр в силу его простоты широко использовался в дипломатической и военной связи несколько веков тому назад. Например, пусть в качестве алфавита сообщений и криптограмм использован алфавит русского языка. Зададим фиксированную функцию вида подстановки :

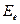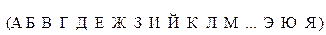
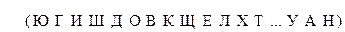
Шифрование достаточно просто: подлежащий шифрованию очередной символ сообщения отыскивается в верхней строке и заменяется на соответствующий (записанный снизу) символ криптограммы. Дешифрование также тривиально и обратно шифрованию.

В шифре перестановки сообщение делится на блоки фиксированной длины 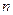и каждый символ переставляется в пределах блока по функции перестановки 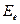. Вид функции перестановки определяется ключом 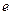. Функция перестановки 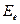, каждый символ блока сообщения, записанный в верхней строке соответствия (4.5), отображает в соответствующий символ блока криптограммы, записанный под ним в нижней строке:

(

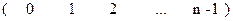
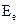
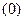
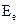
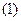
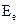
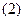
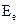
Рассмотренные элементарные шифры подстановки и перестановки сами по себе не способны обеспечить требуемую в современных условиях стойкость криптографических систем, так как они уязвимы к атакам нарушителя на основе частного анализа символов сообщений естественных языков, например таких как телеграфных сообщений, написанных на русском языке. Однако, комбинируя элементарные шифры, можно построить широко используемые на практике стойкие композиционные шифры.

На практике удобно использовать подкласс композиционных шифров, называемый составными шифрами. В составных шифрах над блоком шифруемого сообщения многократно выполняются подстановки и перестановки.

Последовательное использование подстановок и перестановок в составном шифре реализует два основных принципа построения симметричных блочных систем шифрования, сформулированных К. Шенноном: рассеивание и перемешивание.

Рассеивание заключается в распространении влияния всех символов блока открытого сообщения на все символы блока криптограммы, что позволяет скрыть статистические свойства шифруемой информации. Высокая степень рассеивания достигается многократными подстановками, зависящими не только от ключа, но и от значений промежуточных результатов шифрования. Одновременно рассеивание проявляется во влиянии каждого символа ключа на все символы блока криптограммы, что исключает восстановление взаимосвязи статических свойств открытого и шифрованного текста.

Перемешиваниезаключается в усложнении взаимосвязи статических свойств сообщения и полученной из него криптограммы. Высокая степень перемешивания достигается при многократных перестановках в процессе криптопреобразований. Хорошее рассеивание и перемешивание обеспечивается использованием составного шифра, состоящего из последовательности элементарных шифрующих функций, каждая из которых вносит небольшой вклад в значительное суммарное рассеивание и перемешивание.

Современные составные шифры очень часто строятся как итеративные шифры, в которых над блоком сообщения многократно выполняется некоторый набор одних и тех же шифрующих преобразований, называемых круговой функцией шифрования .

Теорема Котельникова (иногда в зарубежной литературе теорема Найквиста) позволяет выделить класс сигналов, для которых эти сигналы могут быть без потерь информации представлены своими дискретными отсчетами.

Мы уже видели, что если в спектре аналоговой сигнала не содержится составляющих с частотами выше частоты Найквиста, то сдвинутые копии спектров не будут прерываться. В этом случае использование идеального ФНЧ с прямоугольной АЧХ позволит выделить исходную (несдвинутую) копию спектра, сосредоточенную в окрестности нулевой частоты и, таким образом, в точности восстановить исходный аналоговый сигнал.

АЧХ идеального ФНЧ для восстановления показана на рисунке. Коэффициент передачи ФНЧ в полосе пропускания равен Т, а не единице, чтобы скомпенсировать множитель 4Т в формуле спектра. С помощью обратного преобразования Фурье находим импульсную характеристику фильтра

Дискретизованный сигнал – это сумма дельта-функций.

При прохождении такого сигнала через восстанавливающий фильтр НЧ каждая дельта-функция породит на выходе соответственно сдвинутую и масштабированную копию импульсной характеристики фильтра. Выходной сигнал (в точности соответствующий исходному аналоговому сигналу) будет представлять собой сумму сдвинутых и умноженных на отсчеты сигнала копий импульсных характеристик идеального ФНЧ

Сформулируем теорему Котельникова: любой сигнал s(t), спектр которого не содержит составляющих с частотами выше некоторого значения ?в = 2?fв (сигнал с финитным, т.е. конечным спектром) может быть без потерь информации представлен своими отсчетами {s(kT)}, взятыми с интервалом Т, удовлетворяющим следующему равенству

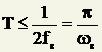
В зарубежной литературе эта теорема называется теоремой Найквиста (Nyquist Theorem) или теоремой дискретизации, теоремой о выборке (sampling theorem).

Последняя формула представляет собой разложение сигнала s(t) в ряд по системе функций {?k(t)}, называемой базис Котельникова

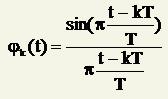
Заметим, что функции всегда называются sinc-функциями.

Контрольные вопросы:

1. Какие шифры вы знаете?

2. Что понимается под подстановкой?

3. Как шифруют методом перестановки?

4. Как им образом шифруют методом перемешивания?

5. Что позволяет сделать теорема Котельникова?