Введение. Вязкость газа или жидкости проявляется в том, что возникшее в среде упорядоченное движение молекул после прекращения действия причин

Вязкость газа или жидкости проявляется в том, что возникшее в среде упорядоченное движение молекул после прекращения действия причин, его вызвавших, постепенно прекращается. Это происходит потому, что между слоями жидкости или газа, движущимися с различными скоростями, действуют силы внутреннего (вязкого) трения, которые стремятся уравнять скорости слоев жидкости.

Сила вязкого трения газов и большинства жидкостей подчиняется закону, установленному И.Ньютоном. Выделим мысленно в потоке жидкости участок ΔS плоскости, в пределах которой скорость упорядоченного движения молекул U(z), зависящая от координаты z, постоянна (рис.1). Сила вязкого трения F, действующая на слой, лежащий выше участка ΔS, будет направлена навстречу движению жидкости и пропорциональна быстроте изменения скорости вдоль оси z Рис. 1 Вязкое трение т.е.перпендикулярно направлению скорости) и также величине площадки ΔS. Количественно, это выражается формулой

(1)

где η – параметр, носящий название динамической вязкости.

С молекулярной точки зрения происхождение сил вязкого трения объясняется следующим образом. Молекулы жидкости или газа участвуют одновременно и в упорядоченном и в хаотическом (тепловом) движении, тепловое движение вызывает перемешивание слоев среды, движущихся с разными скоростями. При этом импульс упорядоченного движения молекул передается от слоев с большей скоростью к слоям с меньшей скоростью. Согласно второму закону Ньютона отличная от нуля скорость изменения импульса выделенного слоя среды означает наличие приложенной к нему силы. Эта сила и называется силой вязкого трения.

Рассмотрим упрощенный расчет коэффициента вязкости в газах. Будем считать скорости теплового движения всех молекул одинаковыми и равными средней тепловой скорости <v>. Само же тепловое движение представим схемой, где все молекулы разделены на шесть одинаковых потоков, параллельных координатным осям. Таким образом, в положительном и отрицательном направлении оси z одинаковое количество молекул, равное одной шестой их общего числа. За время Δt площадку ΔS пересекут те молекулы газа, которые находились на расстояниях меньших, чем Δz = <v>Δt от поверхности. Поэтому число молекул, пересекающих площадку за время Δt,

(2)

где п–- концентрация молекул, Δt – промежуток времени, в течение которого происходит перенос молекул, число которых равно ΔN.

Молекулы газа участвуют кроме теплового движения в упорядоченном движении со скоростью U, которая является непрерывной функцией z. На рис. 1 вектору U соответствует положительное направление оси у. Каждая молекула, пересекая за счет теплового движения поверхность ΔS, переносит импульс упорядоченного движения mU. Поэтому импульс, перенесенный всеми молекулами за время Δt через площадку ΔS в положительном направлении оси z,

ΔР₊ = mU₊ΔN ,

где U₊– характерное значение скорости упорядоченного движения молекул вблизи нижней границы выделенного слоя, т – масса одной молекулы, a ΔN определяется формулой (2). Аналогично импульс, переносимый в отрицательном направлении оси z,

ΔР_{–_}= mU_{–_}ΔN .

Результирующая у – компонента импульса, перенесенная за время Δt через площадку ΔS, равна

ΔР = ΔР₊– ΔР_– = m(U₊ – U_–) ΔN= 1/6 п m<v>(U₊ – U^_) ΔSΔt, (3)

Для нахождения U₊и U_– учтем, что те молекулы газа, которые находятся дальше от площадки ΔS, чем длина свободного пробега, испытывают столкновение с другими молекулами раньше, чем достигнут площадки. Вследствие этого они приобретут скорость упорядоченного движения того слоя газа, где они испытывают столкновение. Таким образом, можно считать, что скорость упорядоченного движения молекул, пересекающих поверхность ΔS в положительном направлении оси z, равна скорости упорядоченного движения U на расстоянии от поверхности ΔS:

U₊ = U_{(z-λ) .}

Скорость упорядоченного движения молекул, пересекающих ΔS в отрицательном направлении оси z, есть

U_– = U_(z+λ) .

Скорость U(z) обычно медленно меняется на расстояниях порядка средней длины свободного пробега λ. Поэтому функцию U_(z±λ) можно разложить в ряд по малой величине λ, ограничившись только линейными членами:

,

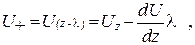
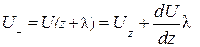откуда

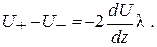
Подставляя это выражение в формулу (3), получим

(4)

Знак минус в этой формуле указывает на направление переноса импульса.

Если 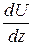> 0, то ΔР < 0, и это означает, что импульс упорядоченного движения переносится в отрицательном направлении оси z, т. е. от быстрых слоев газа к медленным.

Величина силы, действующей на слой газа в пределах поверхности ΔS, равна

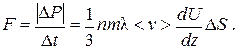
Произведение концентрации п на массу одной молекулы т равно плотности газа ρ, так что окончательное выражение приобретает вид

(5)

Сравнение формулы (5) с законом вязкости Ньютона (1), во-первых, подтверждает справедливость последнего на примере газа. Во-вторых, раскрывает связь коэффициента динамической вязкости

(6)

с молекулярными параметрами системы. Вспоминая, что средняя длина свободного пробега молекул газа равна

⁽⁷⁾

где d – эффективный диаметр молекул, убеждаемся, что произведение не зависит от температуры.

\

где k – постоянная Больцмана, а T - температура. Комбинируя два последних выражения, получаем

Отсюда следует, что коэффициент вязкости газов не зависит от давления и растет с температурой пропорционально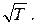

Коэффициент трения жидкости зависит от ее природы (вида молекул), температуры, давления. В отличие от газов, с ростом температуры вязкость жидкости уменьшается. Эта зависимость вязкости жидкости от температуры связана с характером теплового движения молекул.

В жидкости молекулы находятся на расстояниях, соизмеримых с размером молекул, и совершают малые колебания в пределах, ограниченных межмолекулярными расстояниями. Время от времени центр этих колебаний (положения равновесия) совершает случайные скачки, и молекулы перемещаются в новое положение равновесия. За счет этих скачков и происходит передача импульса упорядоченного движения молекул от слоя к слою. С ростом температуры скачки происходит чаще, и жидкость становится более текучей (менее вязкой). Частота скачков пропорциональна exp(–W/kT), где W - энергия, необходимая для скачка.

Коэффициент вязкости жидкости при постоянном давлении зависит от температуры согласно формуле Френкеля – Андраде может быть записан в виде

η = С exp(-W/kT) , (8)

где С – слабая функция от Т.

На твердое тело, движущееся в жидкости, действует сила сопротивления, которая при малых скоростях тела обусловлена силами вязкого трения. Малыми считаются скорости движения, при которых движение жидкости около этого тела имеет ламинарный (не турбулентный) характер. Количественным критерием малости скорости тела является число Рейнольдса

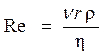
где v – скорость тела, r – характерный размер (например, радиус шара), ρ –плотность жидкости.

Рис. 2. Сопротивление среды

При изучении сопротивления среды (жидкости) движению тела необходимо учитывать вязкое трение отдельных слоев жидкости друг о друга.

Если в неограниченной жидкости движется шарик, то, как показал Стокс, при Re«1 сила сопротивления

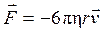
Рассмотрим падение шарика в наполненный жидкостью сосуд с небольшой высоты h (рис. 3).На шарик действуют три силы: сила тяжести mg = ρ_oVg , сила Архимеда F_A = ρVg и сила вязкого трения 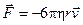.Здесь m - масса шарика, ρ₀ – плотность материала шарика, v – скорость шарика, V – его объем, ρ – плотность жидкости, g – ускорение свободного падения.

Рис. 3. Падение шарика в вязкой жидкости

Второй закон Ньютона для рассматриваемого случая принимает вид

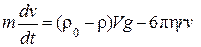. (11)

При движении шарика в воздухе с небольшой скоростью силой вязкого трения шарика о воздух можно пренебречь и определить скорость v₀ у поверхности жидкости, как скорость при свободном падении с некоторой высоты h. Как только шарик погрузится в жидкость, силы вязкого трения и Архимеда возрастут, их сумма окажется больше силы тяжести, и падение будет замедляться (так будет, если высота падения шарика в воздухе достаточно большая). В конечном счете, сумма сил Архимеда и вязкого трения окажется равной силе тяжести. В этом случае ускорение шарика будет равно нулю, скорость движения v = v_s будет постоянна и уравнение (11) примет вид

(ρ – ρ_о) Vg –6πηrv_s = 0 . (12)

Решая уравнение (3) относительно коэффициента ηс учетом того, что V = 4/3πr³ и d = 2r, получаем

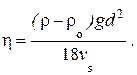(13)

Скорость равномерного движения шарика v_s можно определить, если измерить время прохождения t, пройденное расстояние l и провести расчетпо формуле

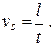(14)

Тогда формула (13) для вычисления коэффициента вязкости преобразуется к виду

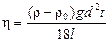. (15)

Таким образом, для определения коэффициента вязкости жидкости необходимо знать плотность жидкости и материала шарика, диаметр шарика и скорость установившегося движения шарика в жидкости, которая может быть измерена экспериментально.