Порядок выполнения работы. Задание I.Измерение диаметра цилиндра
Задание I.Измерение диаметра цилиндра
1. Измерьте 5–7 раз диаметр цилиндра d с помощью микрометра. Результаты измерений занесите в табл. 1.
2. Найдите среднее арифметическое значение диаметра по формуле
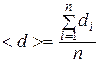 |
,
где п – число измерений, i – номер измерения.
3. Вычислите отклонения результатов отдельных измерений
от среднего арифметического 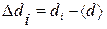 и квадрата отклонения
и квадрата отклонения 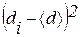 . Занесите результаты в табл. 1.
. Занесите результаты в табл. 1.
Таблица 1
Микрометр №... Цена деления микрометра Δ= 0,01 мм, погрешность прибор δ = 0,01 мм .
| № п/п | 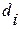
| 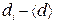
| 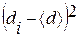
|
| … | |||
| Σ | - | ||
| среднее | - | - |
4. Найдите полуширину доверительного интервала Δd по формуле
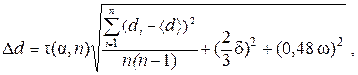 |
где τ(α, n) – коэффициент Стьюдента для заданной доверительной вероятности (чаще всего выбирают α = 0,95; таблица коэффициентов Стьюдента приведена в приложении II), п–- количество измерений, δ – погрешность прибора, Δ – цена деления шкалы прибора.
5. Рассчитайте относительную погрешность εd измерения диаметра цилиндра по формуле
εd = (Δd/< d >) 100% .
6. Результат измерения запишите в стандартном виде:
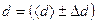 мм, εd= ... при α = 0,95 .
мм, εd= ... при α = 0,95 .
Задание II.Измерение высоты цилиндра
Высоту цилиндра измерьте 5–7 раз с помощью штангенциркуля, данные занесите в табл. 2.
Проведите расчеты погрешности измерения высоты так же, как это было сделано в задании I.
Результат представьте в стандартном виде:
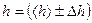 мм, εh = ... при α= 0,95.
мм, εh = ... при α= 0,95.
Таблица 2
Штангенциркуль № ... Цена деления штангенциркуля ω = 0,1мм, погрешность прибора δ = 0,1 мм.
| № п/п | hi | hi – < h > | ( hi – < h >)2 |
| … | |||
| Σ | - | ||
| среднее | - | - |
Задание III. Измерение массы цилиндра
Измерьте массу цилиндра на аналитических весах с ценой деления 1 мг. В этом случае значение массы можно определить с высокой точностью, а погрешность прибора и погрешность округления массы достаточно малы, и поэтому погрешностью в определении массы цилиндра можно пренебречь.
Задание IV.Вычисление плотности цилиндра и оценка
погрешности косвенных измерений
1. Вычислите среднее значение плотности цилиндра по формуле
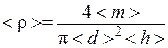 |
,
где < т >, <d>,<h>– средние значения массы, диаметра и высоты цилиндра.
Число p= 3,14159... округлите так, чтобы его относительная погрешность была на порядок (в 10 раз) меньше наибольшей из относительных погрешностей εd,εh,εm. Например, если наибольшая из этих погрешностей больше 13 %, то число следует округлить до двух значащих цифр, т.е. π ≈ 3,1. В этом случае относительная погрешность
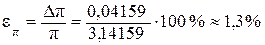 |
.
Если же наибольшая относительная погрешность εd,εh,εm больше 0,5%, но меньше 13%, то число следует округлить до трех значащих цифр: π = 3,14.
При правильном выборе степени округления любой константы (например, числа π) погрешность округления не внесет существенного вклада в величину доверительного интервала измеряемой величины.
2. Рассчитайте относительную погрешность в определении плотности цилиндра по формуле
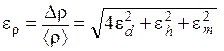 |
.
3. Рассчитайте абсолютную погрешность определения плотности цилиндра
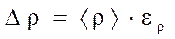 .
.
Результат измерений запишите в стандартном виде:
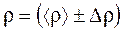 кг/м3,
кг/м3, 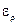 = ... % при α = 0,95
= ... % при α = 0,95
Контрольные вопросы.
1. Что называется плотностью вещества? Укажите размерность плотности и единицы измерения.
2. Прямые и косвенные измерения в данной лабораторной работе.
3. Получите формулы для расчета плотности твердых тел в форме шара и параллелепипеда.
Дата добавления: 2015-09-18; просмотров: 1443;
