Морфологический метод
Данный метод предусматривает поиск всех возможных решений проблемы путем исчерпывающей переписи этих решений. Например, Ф.Р. Матвеев выделяет шесть этапов претворения в жизнь этого метода:
· формулировка и определение ограничений проблемы;
· поиск возможных параметров решений и возможных вариаций этих параметров;
· нахождение всех возможных комбинаций этих параметров в получаемых решениях;
· сравнение решений с точки зрения преследуемых целей;
· выбор решений;
· углубленное изучение отобранных решений.
После завершения этапа генерации идей, приступают к отбору лучших решений. Отбор также может осуществляться группой экспертов. Варианты решения, сравниваются с идеальной моделью решения. Производится отсев всех непригодных вариантов и выбор решения. Другими словами, сначала поле писка расширяется, а затем сужается до одного варианта.
Метод «Дельфи» первоначально был предложен как одна из процедур при проведении мозговой атаки и должен был помочь снизить степень влияния психологических факторов и повысить объективность оценок экспертов. Затем метод стал использоваться самостоятельно. Его основа – обратная связь, ознакомление экспертов с результатами предшествующего этапа и учёт этих результатов экспертами при оценке значимости. Этапы метода «Дельфи» следующие:
· осуществляется поиск экспертов;
· каждому эксперту предлагается один и тот же вопрос;
· каждый эксперт вырабатывает свои оценки независимо от других экспертов;
· ответы собираются и статистически усредняются;
· экспертам, ответы которых сильно отклоняются от средних значений, предлагается обосновать свои оценки;
· эксперты разрабатывают обоснования и выносят их на рассмотрение;
· среднее значение и соответствующие обоснования предъявляются всем экспертам;
· процедура повторяется до минимального расхождения мнений.
Эвристические методы, взламывающие психологический барьер, свою задачу выполняют достаточно успешно. С их помощью можно получить от несколько десятков до сотен тысяч вариантов решения проблемы (особенно эффективен в этом отношении морфологический анализ). Однако тут же возникает новая проблема, как из этой массы вариантов выбрать наиболее предпочтительный вариант?
Преодолеть барьер перебора большого числа вариантов, даже с помощью ЭВМ, задача далеко не простая. Поэтому, например, в математическом программировании высоко ценятся методы, позволяющие резко сократить количество рассматриваемых случаев. Необходимость в ограничении перебора настолько велика, что в рамках строгих математических методов начинают широко пользоваться приближёнными, эвристическими методами.
Как только возникает необходимость одновременного рассмотрения более 7-10 вариантов, человек испытывает психологический дискомфорт. Ясно, что расширение поля поиска должно быть минимальным и в тоже время должно перекрывать область оптимального решения. Такой поиск называется направленным. Он наиболее рационален, экономичен и эффективен. Реализовать направленный поиск можно путём ступенчатого расширения и сужения поля поиска по уровням дерева целей-средств, при движении от цели (вершины) к вариантам их осуществления.
Подход аналитической иерархии (Analytic Hierarchy Process - АНР) широко известен в настоящее время. В случае небольшого числа заданных альтернатив представляется разумным направить усилия ЛПР на сравнение только заданных альтернатив. Именно такая идея лежит в основе метода АНР.
1. Основные этапы подхода АНР
Постановка задачи, решаемой с помощью метода АНР, заключается обычно в следующем.
Дано: общая цель (или цели) решения задачи; критерии оценки альтернатив; альтернативы.
Требуется: выбрать наилучшую альтернативу.
Подход АНР состоит из совокупности этапов.
1. Первый этап заключается в структуризации задачи в виде иерархической структуры с несколькими уровнями: цели – критерии—альтернативы.
2. На втором этапе ЛПР выполняет попарные сравнения элементов каждого уровня. Результаты сравнений переводятся в числа.
3. Вычисляются коэффициенты важности для элементов каждого уровня. При этом проверяется согласованность суждений ЛПР.
4. Подсчитывается количественный индикатор качества каждой из альтернатив и определяется наилучшая альтернатива.
Рассмотрим эти этапы подробнее применительно к основному методу АНР, разработанному Т.Саати, используя для иллюстрации пример выбора площадки для строительства аэропорта.
2. Структуризация
Предположим, что комиссия по выбору места постройки аэропорта предварительно отобрала из нескольких возможных три варианта: А, В, К. Тогда структура решаемой задачи может быть представлена в виде, показанном на рис. 1.
Цели
Цель строительства аэропорта
прием и отправка большого числа пассажиров
Критерии
Стоимость строительства
Время в пути от аэропорта до центра города
Количество людей, подвергающихся шумовым воздействиям
Альтернативы
Площадка А Площадка В Площадка К
Рис. 1. Иерархическая схема проблемы выбора места для аэропората
3. Попарные сравнения
При попарных сравнениях в распоряжение ЛПР дается шкала словесных определений уровня важности, причем каждому определению ставится в соответствие число (табл. 8).
Т а б л и ц а 8 – Шкала относительной важности
| Уровень важности | Количественное значение |
| Равная важность | |
| Умеренное превосходство | |
| Существенное или сильное превосходство | |
| Значительное (большое) превосходство | |
| Очень большое превосходство |
При сравнении элементов, принадлежащих одному уровню иерархии, ЛПР выражает свое мнение, используя одно из приведенных в табл. 8 определений. В матрицу сравнения заносится соответствующее число. Матрица сравнений критериев выбора площадки для аэропорта приведена в табл. 9.
Т а б л и ц а 9 – Матрица сравнений для критериев
| Критерии | C1 Стоимость | С2 Время в пути до центра города | С3 Количество людей, подвергающихся шумовым воздействиям | Собственный вектор |
| C1 Стоимость | 2,47 | |||
| С2 Время в пути до центра города | 1/5 | 0,848 | ||
| С3 Количество людей, подвергающихся шумовым воздействиям | 1/3 | 1/3 | 0,48 |
Матрица соответствует следующим предпочтениям гипотетического ЛПР: критерий «Стоимость» существенно превосходит критерий «Время в пути» и умеренно превосходит критерий «Количество людей, подвергающихся шумовым воздействиям»; критерий С2 умеренно превосходит критерий С3. На нижнем уровне иерархической схемы сравниваются заданные альтернативы (конкретные площадки) по каждому критерию отдельно. Приведем эти сравнения в табл. 10.
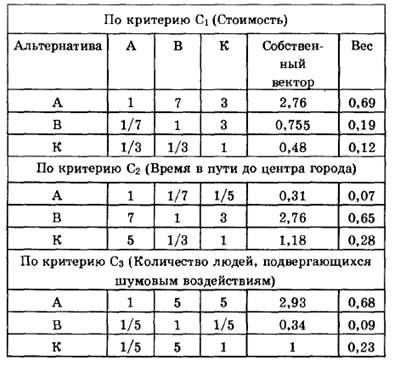
Таблица 10 – Относительная важность альтернатив по отдельным критериям
4. Вычисление коэффициентов важности
Таблицы 9 и 10 позволяют рассчитать коэффициенты важности соответствующих элементов иерархического уровня. Для этого нужно вычислить собственные векторы матрицы, а затем пронормировать их. Формула для этих вычислений: извлекается корень п-й степени (п — размерность матрицы сравнений) из произведений элементов каждой строки. Так, из табл. 9 определяются коэффициенты важности критериев. В последнем столбце таблицы приведены значения собственных векторов. Нормирование этих чисел дает: w1=0,65; w2=0,22; w3=0,13, где wi - вес i-го критерия.
Таким же способом на основе табл. 10 можно рассчитать важность каждой из площадок по каждому из критериев. В таблице приведены веса соответствующей площадки по каждому из критериев.
В книге Т. Саати (автора метода АНР) дается способ проверки согласованности суждений ЛПР при заполнении каждой из матриц - путем сравнения со случайно заполненной матрицей.
Ясно, что при сравнительно небольших ошибках ЛПР условие согласованности выполняется.
5. Определение наилучшей альтернативы
Синтез полученных коэффициентов важности осуществляется по формуле:
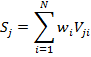
где S — показатель качества j-й альтернативы; wi — вес i-гo критерия; Vji— важность j-й альтернативы по i-му критерию.
Для трех площадок проведенные вычисления позволяют определить:
SA= 0,65 × 0,69 + 0,22 × 0,07 + 0,13 × 0,68 = 0,552;
SB = 0,65 × 0,19 + 0,22 × 0,65 + 0,13 × 8) 0,09 = 0,278;
SK= 0,65 × 0,12 + 0,22 × 0,28 + 0,13 × 0,23 = 0,17.
Итак, альтернатива А оказалась лучшей.
Группа методов (ЭЛЕКТРА I, ЭЛЕКТРА II, ЭЛЕКТРА III) была разработана коллективом французских ученых, возглавляемым профессором Б. Руа. В этих методах бинарное отношение предпочтения, более сильное, чем отношение Парето, строится следующим образом.
Для каждого из n критериев (предполагается, что критерии числовые) определяется вес – число, характеризующее важность соответствующего критерия, которое тем больше, чем важнее для ЛПР соответствующий критерий. Эти веса могут быть определены либо ранжированием, либо, например, по методу Саати. Для того, чтобы определить, превосходит альтернативный вариант 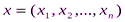 , вариант
, вариант  (где
(где  - значения i-го критерия, сообщаемые ему вариантами х и у соответственно), производятся следующие действия.
- значения i-го критерия, сообщаемые ему вариантами х и у соответственно), производятся следующие действия.
Множество I критериев разбивается на три подмножества:
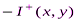 – критерии, по которым х превосходит у;
– критерии, по которым х превосходит у;
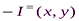 – критерии, по которым х и у имеют одинаковые оценки;
– критерии, по которым х и у имеют одинаковые оценки;
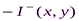 – критерии, по которым у превосходит х.
– критерии, по которым у превосходит х.
Далее определяется относительная важность  ,
, 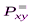 ,
, 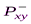 каждого из этих подмножеств
каждого из этих подмножеств
 (5.1)
(5.1)
Устанавливается также некоторый порог с и считается, что вариант х превосходит вариант у только в том случае, когда некоторая функция, называемая индексом согласия, удовлетворяет условию 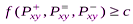 (5.2)
(5.2)
Вид функции  определяется по своему для каждой модификации метода ЭЛЕКТРА.
определяется по своему для каждой модификации метода ЭЛЕКТРА.
В качестве условия (5.2) в методе ЭЛЕКТРА I предлагается рассматривать выражение вида:
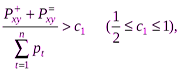 (5.3)
(5.3)
в методе ЭЛЕКТРА II – выражение вида
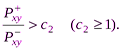 (5.4)
(5.4)
Следует отметить, что условие (5.3) можно применять лишь тогда, когда сравнение альтернатив происходит в строгих шкалах (тогда множество 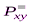 пусто) или когда число совпадающих оценок у различных вариантов достаточно мало по сравнению с n. В противном случае отношение предпочтения, может оказаться симметричным: x лучше у (хRу) и у лучше х (уRх) одновременно. Поэтому, если используются нестрогие шкалы, то лучше пользоваться условием (5.4).
пусто) или когда число совпадающих оценок у различных вариантов достаточно мало по сравнению с n. В противном случае отношение предпочтения, может оказаться симметричным: x лучше у (хRу) и у лучше х (уRх) одновременно. Поэтому, если используются нестрогие шкалы, то лучше пользоваться условием (5.4).
Условие (5.2) является необходимым, но не достаточным условием превосходства х над у. В методах ЭЛЕКТРА формулируются дополнительные условия, предназначенные учитывать не только порядок следования оценок х и у по критериям, но и значения модулей разностей 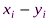 . Эти условия, называемые индексом несогласия, могут быть записаны в виде
. Эти условия, называемые индексом несогласия, могут быть записаны в виде 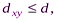 (5.5), где
(5.5), где 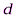 – пороговое значение индекса несогласия
– пороговое значение индекса несогласия  .
.
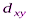 для каждой модификации метода ЭЛЕКТРА определяются по-своему.
для каждой модификации метода ЭЛЕКТРА определяются по-своему.
Таким образом, отношение предпочтения  определяется следующим образом:
определяется следующим образом:
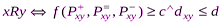 (5.6)
(5.6)
Особенность методов ЭЛЕКТРА состоит в том, что в них несколько отступают от традиционных методов выделения подмножества недоминируемых вариантов. Следуя теории игр, их создатели предлагают несколько расширить это подмножество путем выделения в исходном множестве некоего ядра, все элементы которого несравнимы между собой, а любой вариант, в ядро не вошедший, доминируется хотя бы одним элементом ядра.
Выделение ядра на множестве исходных вариантов является заключительным этапом методов ЭЛЕКТРА. Дальнейшее сужение ядра может быть достигнуто заданием других, более жестких ограничений в условиях (5.2) и (5.5), т. е. увеличением порогового значения индекса согласия с и уменьшением порогового значения индекса несогласия d.
Пусть в исходном множестве альтернативных вариантов, сравниваемых по пяти критериям, определены следующие семь недоминируемых по Парето:
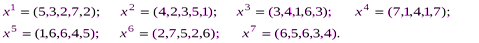
Применим метод ЭЛЕКТРА для того, чтобы, получив у ЛПР дополнительную информацию, сократить число вариантов, которое будет предложено ему для окончательного выбора.
1-й этап. От ЛПР получается информация о сравнительной важности критериев. Пусть ЛПР сообщил, что:
– критерии 1 и 2 имеют одинаковую важность;
– критерии 3, 4 и 5 имеют также одинаковую важность;
– каждый из первых двух критериев важнее каждого из оставшихся.
Пусть в соответствии с этой информацией критериям назначены веса:
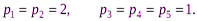
2-й этап. Строим матрицу 7*7, в которой элемент atj определяется следующим образом:
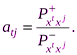
Допустим, что в качестве порогового значения индекса согласия выбрано на основе консультаций с ЛПР c2 = 1,25. Как видно из таблицы 5.1, любой из семи вариантов доминируется хотя бы одним из остальных.
Таблица 5.1 – Матрица значений atj
| – | 1,3 | 0,75 | 0,75 | 0,75 | 0,17 | |
| 0,17 | – | 0,75 | 0,75 | 0,75 | 0,75 | 0,17 |
| 0,75 | 1,3 | – | 0,75 | 0,75 | 0,75 | 0,17 |
| 1,3 | 1,3 | 1,3 | – | 0,75 | 0,75 | 0,75 |
| 1,3 | 1,3 | 1,3 | 1,3 | – | 0,4 | 1,3 |
| 1,3 | 1,3 | 1,3 | 1,3 | 2,5 | – | 0,75 |
| 1,3 | 0,75 | 1,3 | – |
Поэтому без учета индекса несогласия подмножество оптимальных вариантов оказалось бы пустым.
3-й этап. С помощью ЛПР устанавливается индекс несогласия. Пусть
D = {(х, у): xt – уt > 5}.
В этом случае один из вариантов – х7 - оказывается недоминируемым, оптимальным будет считаться также и вариант х5, который несравним с х7.
Таким образом, применение метода ЭЛЕКТРА позволило более полно учесть мнение ЛПР и сократить исходное множество решений до двух элементов.
Дата добавления: 2015-09-18; просмотров: 912;
