Перпендикулярные прямые

Рассмотрим теорему: если одна сторона прямого угла параллельна плоскости проекций (или лежит в ней), то прямой угол проецируется на эту плоскость без искажения.

Приведем доказательство для прямого угла ABC, одна сторона которого ВС параллельна горизонтальной плоскости (рис. 32).

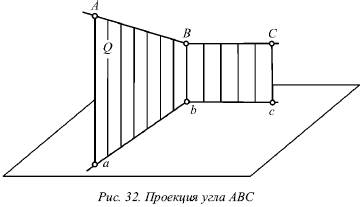
Плоскость, в которой находится сторона угла АВ и ее проекция ab, перпендикулярна горизонтальной плоскости, так как содержит перпендикуляр Вb к этой плоскости. Прямая ВС перпендикулярна плоскости Q вследствие ее перпендикулярности двум пересекающимся прямым этой плоскости (АВ и Вb). Прямая bc параллельна ВС, т. е. она также перпендикулярна Q, а значит и прямой ab, которая лежит в ней.

Ясно, что если на эпюре одна пара одноименных проекций двух прямых перпендикулярна, а одна из двух остальных проекций параллельна оси х, то такие прямые образуют в пространстве прямой угол.

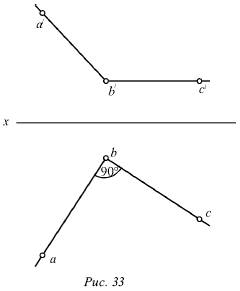
Предположим, что ab ⊥bc, b́с́ || x.

Это показано на рисунке 33.

Можно провести через проекцию аb плоскость Q, проектирующую прямую АВ на горизонтальную плоскость (рис. 33). Проекция bс перпендикулярна плоскости Q вследствие того, что она перпендикулярна двум прямым этой плоскости, т. е. проекции аb (по условию), и проецирующему лучу Вb как перпендикуляру горизонтальной плоскости.

Прямая ВС является параллельной горизонтальной плоскости, так как ее фронтальная проекция bс параллельна оси х, поэтому она параллельна своей горизонтальной проекции, т. е. справедливо выражение ВС || bс. Следовательно, прямая ВС перпендикулярна плоскости Q и поэтому перпендикулярна прямой АВ вне зависимости от ее положения в плоскости Q.

Через некоторую точку М можно провести огромное количество прямых, которые перпендикулярны данной прямой АВ. Они образуют целую плоскость Р, перпендикулярную АВ (рис. 34).

Из всех перпендикулярных прямых, которые при этом образуются, только одна пересекает данную прямую. Это прямая MN, которая проходит через точку N пересечения прямой АВ и плоскости Р.

Под перпендикуляром к прямой подразумевается прямая, не только перпендикулярная данной прямой, но и пересекающая в отличие от просто перпендикулярных скрещивающиеся прямые.

Прямой угол между скрещивающимися прямыми проецируется на данную плоскость проекций без искажения, если одна из прямых параллельна этой плоскости или лежит в ней.