Линиями наибольшего уклона (ЛНУ) плоскости называются прямые перпендикулярные линиям уровня этой плоскости.

Прямые в плоскости, перпендикулярные горизонталям этой плоскости называют часто линиями наибольшего ската (по этим линиям стекают с крыши дома капли дождя), они образуют наибольший угол с горизонтальной плоскостью.

Действительно, если провести в плоскости Б(рисунок 2-7) прямую АВ, перпендикулярную к горизонтали h этой плоскости и произвольную прямую АС, то нетрудно показать, что прямая АВ образует больший угол наклона с горизонтальной плоскостью Г, нежели прямая АС.Покажем, что a>b.

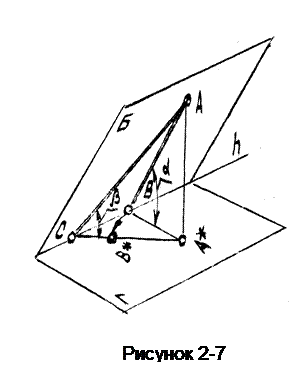Рассмотрим два прямоугольных треугольника: DАА*В и DАА*С с общим катетом АА*. Здесь АВ меньше АС, т.к. АВ- перпендикуляр из точки А на прямую h, в то время как АС - наклонная к h линия. Поэтому если совместить поворотом DАА*В с DАА*С,то прямая АВ займет положение АВ* внутри DАА*С и станет очевидно, что ÐABA*=a>ÐACA*=b

Аналогично можно показать, что прямая плоскости, перпендикулярная к фронтали или профильной прямой данной плоскости, является соответственно прямой наибольшего уклона к фронтальной или профильной плоскости уровня.

Нетрудно видеть, что линейный угол между ЛНУ и ее проекцией А*В* является равным углу наклона плоскости Б к плоскости Г. Поэтому: измерение двугранного угла между плоскостью общего положения Б и плоскостью уровня сводится к измерению угла между соответствующей прямой наибольшего уклона плоскости Б и проекцией ЛНУ на выбранную плоскость уровня.

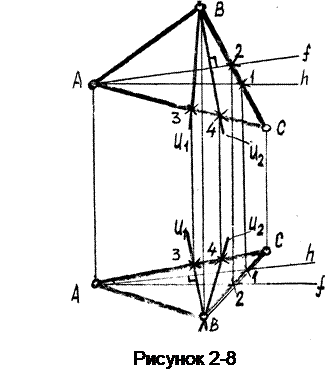
Пример 1. Провести в плоскости Б (D АВС) через точку В прямые наибольшего уклона U1 и U2 к горизонтальной и фронтальной плоскостям (рисунок 2-8). Сначала строим ЛНУ к горизонтальной плоскости. Для этого в заданной плоскости Б проведем горизонталь h- например А-1;На предыдущем рисунке 3-2 видно, что перпендикулярность к h сохраняется и на виде сверху (аналогично перпендикулярность кf сохраняется на виде спереди; пока без доказательства).

Учитывая сказанное, проводим ЛНУ U1 сначала на виде сверху, а затем (используя т.2) и на виде спереди. Выделив на линии наибольшего уклона к горизонтальной плоскости отрезок (например B-2), найдем угол его наклона к Г плоскости способом прямоугольного треугольника.

Аналогичным образом строим ЛНУ к Ф плоскости и находим угол наклона ее (а значит и плоскости) к Ф плоскости.

5. Прямые общего положения

Прямая не параллельная ни одной из плоскостей уровня называется прямой общего положения.

Различают восходящие и нисходящиепрямые общего положения.

Восходящая прямая по мере удаления от наблюдателя идет вверх (рисунок 2-9а).

Нисходящая прямая - по мере удаления от наблюдателя такая прямая понижается (рисунок 2-9б).

Реконструируем прямые. Замечаем, что на комплексном чертеже проекции восходящей прямой ориентированы одинаково, а проекции нисходящей имеют различную ориентацию.

Любой отрезок, принадлежащий таким прямым, на всех проекциях отображается с искажением.