Стеганопреобразование как возмущение матрицы контейнера
Как основное сообщение (ОС), или контейнер, для удобства изложения рассматривается изображение в градациях серого, прямоугольная (или квадратная) матрица которого обозначается 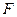 .
.
Погружение ДИ в ОС – стеганопреобразование ОС независимо от способа и области этого погружения можно представить как возмущение 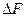 матрицы
матрицы 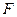 . Тогда матрица СС
. Тогда матрица СС 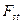 удовлетворяет соотношению:
удовлетворяет соотношению:
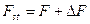 , (5.1)
, (5.1)
где 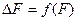 , т.е.
, т.е. 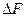 - это некоторая функция матрицы контейнера
- это некоторая функция матрицы контейнера 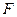 . Исходя из формулы (5.1), каждое стеганопреобразование можно представить в виде аддитивного погружения некоторой информации в пространственной области ОС. Любые преобразования, которые после погружения ДИ происходят со СС, будем рассматривать как дополнительные возмущения матрицы
. Исходя из формулы (5.1), каждое стеганопреобразование можно представить в виде аддитивного погружения некоторой информации в пространственной области ОС. Любые преобразования, которые после погружения ДИ происходят со СС, будем рассматривать как дополнительные возмущения матрицы 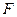 . Таким образом, стеганопреобразованте изображения, результаты атак, которые происходят во время пересылки СС по каналу связи и т.д. представляются в виде элементарных матричных операций.
. Таким образом, стеганопреобразованте изображения, результаты атак, которые происходят во время пересылки СС по каналу связи и т.д. представляются в виде элементарных матричных операций.
Определим один из возможных наборов формальных параметров, который полностью определяет любое ОС и СС (ЦИ). параметров можно использовать множество сингулярных чисел и ортонормированных лексикографически положительных сингулярных векторов, а также спектр (совокупность собственных значений) и множество ортонормированных лексикографически положительных собственных векторов (СВ) соответствующей матрицы. Отдадим предпочтение второму набору параметров для симметричной квадратной матрицы 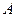 размерами
размерами 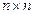 благодаря следующим замечаниям:
благодаря следующим замечаниям:
1) построение спектрального разложения (2.3) симметричной матрицы имеет ряд преимуществ, в сравнении с построением сингулярного разложения, для матрицы произвольной структуры тех же размеров;
2) собственные значения (СЗ) симметричной матрицы являються хорошо обумовленнями в соответствии с формулой:
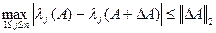 ,
,
где 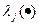 - СЗ соответствующей матрицы,
- СЗ соответствующей матрицы, 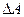 - матрица возмущения
- матрица возмущения 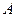 ,
, 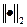 - спектральная матричная норма (СМН), т.е. задача нахождения СЗ симметричной матрицы является нечувствительной к погрешностям входных данных, чего нельзя утверждать в общем случае для несимметричных матриц;
- спектральная матричная норма (СМН), т.е. задача нахождения СЗ симметричной матрицы является нечувствительной к погрешностям входных данных, чего нельзя утверждать в общем случае для несимметричных матриц;
3) использование симметричной матрицы контейнера позволяет значительно увеличить пропускную способность некоторых стеганографических алгоритмов по сравнению с несимметричным вариантом контейнера.
Если 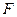 - произвольная квадратная матрица ОС,
- произвольная квадратная матрица ОС, 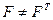 , поставим в соответствие матрице
, поставим в соответствие матрице 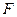 две симметричные матрицы тех же размеров по правилу (2.4):
две симметричные матрицы тех же размеров по правилу (2.4):
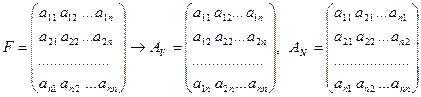 (5.2)
(5.2)
Формула (5.2) дает принципиальную возможность рассматривать матрицу ОС как симметричную матрицу, характеристиками которой являются СЗ и СВ, что и делается дальше. Формирование матрицы СС происходит с использованием верхнего треугольника 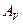 и нижнего треугольника матрицы
и нижнего треугольника матрицы 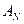 .
.
Дата добавления: 2015-09-18; просмотров: 943;
