Полная система уравнений Максвелла
Применяя теоремы Стокса и Остроградского–Гаусса:
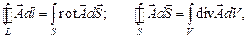
можно представить полную систему уравнений Максвелла в дифференциальной форме, характеризующих поле в каждой точке пространства:
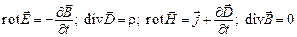 . (4.6)
. (4.6)
Необходимо указать связь между векторами 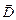 ,
, 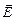 ,
, 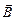 и
и 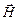 , т.е. конкретизировать свойства материальной среды, в которой рассматривается электромагнитное поле. Уравнения, связывающие эти величины, называются материальными уравнениями:
, т.е. конкретизировать свойства материальной среды, в которой рассматривается электромагнитное поле. Уравнения, связывающие эти величины, называются материальными уравнениями:
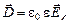
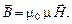 (4.7)
(4.7)
К материальным уравнениям относится и закон Ома в дифференциальной форме: 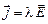 , где
, где 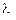 – удельная проводимость вещества.
– удельная проводимость вещества.
Замкнутая система уравнений Максвелла представлена в табл. 4.2.
Таблица 4.2
| Интегральная форма | Дифференциальная форма |
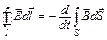
| 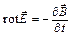
|
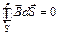
| 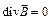
|
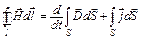
| 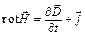
|
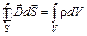
| 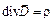
|
| Материальные уравнения | |
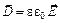 , , 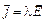
| 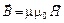
|
Дата добавления: 2015-09-18; просмотров: 853;
