Природа носителей тока в металлах

Классическая теория электропроводности металлов основывается на представлении о существовании в металлах свободных электронов.

Доказательством электронной природы тока в металлах является опыт Рикке (1901 г.). Через три последовательно соединенных цилиндра (два алюминиевых и один медный) с тщательно отшлифованными торцами пропускался длительное время ток. До и после эксперимента цилиндры были точно взвешены. Отличия в массах обнаружено не было. Был сделан вывод, что пропускание тока не оказало на цилиндры никакого влияния. При исследовании соприкасавшихся торцов под микроскопом также не было обнаружено проникновения одного металла в другой. Отсюда следовал вывод: перенос заряда в металлах осуществляется не атомами, а частицами, входящими в состав всех металлов, и тогда предположили, что это электроны.

Для доказательства, что носителями тока являются электроны необходимо определить знак и удельный заряд частиц. Были проведены опыты, они основывались на следующем: если в металлах имеются легко перемещающиеся частицы, то при торможении металлического проводника эти частицы должны некоторое время двигаться по инерции, в результате чего в проводнике возникнет кратковременный ток.

Первый опыт с ускоренно движущимися проводниками был поставлен Мандельштамом и Папалекси (1913 г.). Катушку с проводом приводили в быстрые крутильные колебания вокруг ее оси. К концам катушки подключали телефон, в котором был слышен звук, вызванный импульсами тока.

Количественный результат был получен Стюартом и Толменом (1916 г.), измерявшими импульсы тока, возникающего при резком торможении катушки с проводом.

Эти опыты экспериментально доказали, что носителями заряда в металлах являются электроны.

5.2. Основные положения классической
электронной теории проводимости металлов

П. Друде разработал теорию электропроводности металлов, которую затем усовершенствовал Г.А. Лоренц. Объяснение различных свойств вещества существованием и движением в нем электронов составляет содержание электронной теории. Классическая электронная теория предполагает следующее.

1. Движение электронов подчиняется законам классической механики.

2. Электроны друг с другом не взаимодействуют.

3. Электроны взаимодействуют только с ионами кристаллической решетки, взаимодействие это сводится только к соударениям.

4. В промежутках между соударениями электроны движутся совершенно свободно.

5. Электроны проводимости рассматривают как электронный газ, подобно идеальному газу; идеальный газ подчиняется закону равномерного распределения энергии по степеням свободы, этому же закону подчиняется и электронный газ.

Классическая электронная теория хорошо объясняет существование сопротивления материалов, законы Ома и Джоуля–Ленца, позволяет выразить удельную электропроводность через атомарные постоянные металла, объясняет, по крайней мере качественно, зависимость электропроводности от температуры и позволяет понять связь тепло- и электропроводности металлов. Эта теория объясняет и другие электрические и оптические свойства вещества. Однако в некоторых случаях классическая электронная теория приводит к выводам, находящимся в противоречии с опытом. Например, из теории получается, что удельное сопротивление с увеличением температуры должно возрастать пропорционально 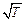. Опыт подтверждает прямо пропорциональную зависимость 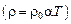. В классической электронной теории теплоемкость материалов и явление сверхпроводимости совершенно необъяснимы.

Трудности классической электронной теории заключаются в следующем:

а) электроны проводимости не подчиняются законам статистики Максвелла — Больцмана;

б) не учитывается взаимодействие электронов друг с другом;

в) не учитывается, что электроны движутся в периодическом поле кристаллической решетки;

г) движение электронов описывается не законами классической механики, а законами квантовой механики.

На смену классической электронной теории пришла квантовая теория твердых тел, в которой преодолены трудности клас­сической теории. Надо отметить, что классическую электронную теорию применяют и сейчас, так как она проста и наглядна, а при малых концентрациях носителей заряда и больших температурах квантовая и классическая теории дают близкие результаты.

5.3.Законы Ома и Джоуля–Ленца по классической теории

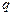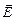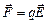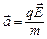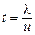Заряд , помещенный в электрическое поле напряженностью , испытывает действие силы и приобретает ускорение , т.е. движение не является равномерным. При столкновении с ионами электроны теряют скорость, и затем под действием сил поля вновь ускоряются до , где – время свободного пробега между соударениями, 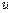– скорость хаотического движения, 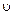– скорость движения электронов , 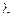– длина свободного пробега между соударениями.

Отсюда 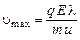, тогда средняя скорость 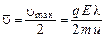. С учетом этого выражение для плотности тока:

,

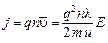где – заряд и масса электрона; 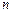– число электронов в единице объема; 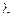– длина свободного пробега; 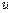– скорость хаотического движения электронов.

Если обозначить 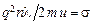, то выражение для плотности тока примет вид: 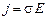. Это соотношение совпадает с экспериментальным законом Ома в дифференциальной форме.

Выведем закон Джоуля–Ленца на основе классической теории. Энергия, приобретенная электроном в поле напряженностью 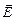за время между двумя столкновениями с ионами кристаллической решетки равна: , где 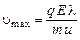– скорость электрона перед столкновением с узлом кристаллической решетки, как это было показано выше при выводе закона Ома.

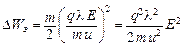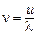Отсюда: . За секунду электрон испытывает столкновений: . Энергия, сообщаемая одним электроном ионной решетке за одну секунду, равна:

.

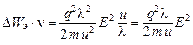В единице объема содержится 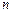свободных электронов, за одну секунду они сообщат ионной решетке энергию:

.

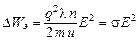Эта формула, полученная на основе классической электронной теории, аналогична экспериментальному закону Джоуля–Ленца в дифференциальной форме.