Энергия магнитного поля. Плотность энергии
После размыкания ключа через гальванометр некоторое время течет убывающий ток. Работа этого тока равна работе сторонних сил, роль которых выполняет ЭДС самоиндукции 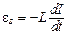 , действующая в контуре. Пусть за время
, действующая в контуре. Пусть за время 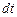 по цепи переносится заряд
по цепи переносится заряд 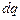 .
.
Работа тока самоиндукции по перемещению этого заряда:
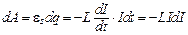 .
.
Проинтегрировав это выражение, получим полную работу тока:
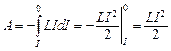 .
.
Совершение этой работы сопровождается исчезновением магнитного поля, которое первоначально существовало в соленоиде и окружающем его пространстве. Отсюда можно сделать вывод, что магнитное поле является носителем той энергии, за счет которой производится работа тока, идущая на изменение внутренней энергии проводников – их нагревание. Таким образом, проводник, имеющий индуктивность 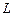 , обладает энергией
, обладает энергией
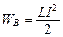 .
.
Заменив, индуктивность соленоида 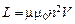 и напряженность магнитного поля соленоида
и напряженность магнитного поля соленоида 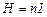 , получим:
, получим:
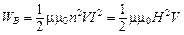 .
.
Если учесть, что 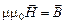 , то выражение для энергии магнитного поля:
, то выражение для энергии магнитного поля: 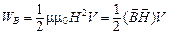 .
.
Энергия единицы объема поля, или плотность энергии магнитного поля
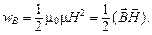
Если магнитное поле неоднородно, то чтобы найти энергию поля в некотором объеме 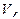 нужно вычислить интеграл:
нужно вычислить интеграл:
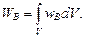
Дата добавления: 2015-09-18; просмотров: 837;
