Розв’язування систем трьох лінійних рівнянь за формулами Крамера. Однорідні системи
Нехай задана система
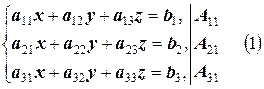
з якої необхідно знайти 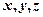 при відомих інших елементах.
при відомих інших елементах.
Складемо визначник системи із коефіцієнтів при невідомих
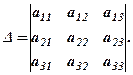
Домножимо почленно кожне з рівнянь відповідно на 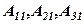 - алгебраїчні доповнення елементів першого стовпця (коефіцієнтів при х) і додамо всі три рівності. Отримаємо:
- алгебраїчні доповнення елементів першого стовпця (коефіцієнтів при х) і додамо всі три рівності. Отримаємо:
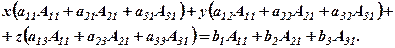
За теоремою про розклад коефіцієнт при х дорівнює 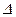 . Коефіцієнти при
. Коефіцієнти при 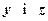 будуть рівними нулю за теоремою анулювання. Права частина рівності за теоремою про заміщення дає новий визначник, який називають допоміжним і позначають
будуть рівними нулю за теоремою анулювання. Права частина рівності за теоремою про заміщення дає новий визначник, який називають допоміжним і позначають
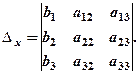
Після цього остання рівність запишеться
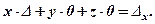 (2)
(2)
Для знаходження 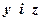 домножимо кожне з рівнянь початкової системи в першому випадку відповідно на
домножимо кожне з рівнянь початкової системи в першому випадку відповідно на 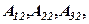 в другому - на
в другому - на 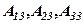 і додамо. В наслідок перетворень отримаємо:
і додамо. В наслідок перетворень отримаємо:
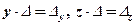
де
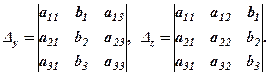
Якщо 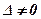 , то в результаті отримуємо формули Крамера:
, то в результаті отримуємо формули Крамера:
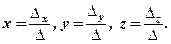
Окремим випадком системи (1) є однорідна система
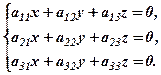 (3)
(3)
Серед розв’язків однорідної системи можуть бути як нульові розв’язки 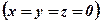 , так і розв’язки відмінні від нуля.
, так і розв’язки відмінні від нуля.
Теорема 1. Якщо визначник 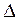 однорідної системи (3) відмінний від нуля (
однорідної системи (3) відмінний від нуля ( 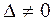 ), то така система має тільки нульовий розв’язок.
), то така система має тільки нульовий розв’язок.
Дійсно, за властивістю 4 в 1.3. допоміжні визначники 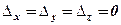 , як такі, що містять нульовий стовпець, тому за формулами Крамера
, як такі, що містять нульовий стовпець, тому за формулами Крамера 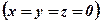 .
.
Теорема 2. Якщо однорідна система має відмінний від нуля розв’язок, то її визначник 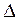 необхідно дорівнює нулю
необхідно дорівнює нулю 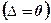 .
.
Дійсно, нехай одне з невідомих, наприклад х, відмінне від нуля. Згідно з однорідністю 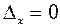 . Рівність (2) запишеться
. Рівність (2) запишеться 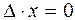 . Звідки випливає, що
. Звідки випливає, що 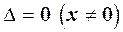 .
.
Дата добавления: 2015-09-18; просмотров: 842;
