Кінематика обертового руху
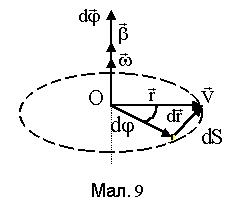
Обертовий рух точки (див. Мал. 9) визначається кутом повороту радіус-вектора положення тіла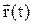 . Елементарний поворот
. Елементарний поворот 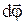 визначається як вектор, що лежить на осі обертання, причому обертання тіла відбувається проти годинникової стрілки, якщо його спостерігати з кінця вектора
визначається як вектор, що лежить на осі обертання, причому обертання тіла відбувається проти годинникової стрілки, якщо його спостерігати з кінця вектора 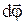 . Цей вектор задовольняє аксіомам алгебри векторів. Однак, скінчені повороти j не задовольняють цим аксіомам і не можуть представлятися векторами. Вектор переміщення
. Цей вектор задовольняє аксіомам алгебри векторів. Однак, скінчені повороти j не задовольняють цим аксіомам і не можуть представлятися векторами. Вектор переміщення 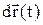 за величиною можна визначити як dr=rdj.
за величиною можна визначити як dr=rdj.
Кутова швидкістьє похідною від кута повороту радіус-вектора 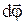
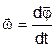 ,
,
її вектор лежить на вісі обертання і паралельний вектору 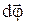 . Кутове прискорення
. Кутове прискорення 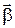 визначається як
визначається як
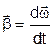
і є вектором, паралельним вектору кутової швидкості.
Одиницею вимірювання величини кутової швидкості є рад/с, а кутового прискорення - рад/с2.
Лінійна швидкість 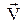 обертового руху дорівнює векторному добуткові кутової швидкості
обертового руху дорівнює векторному добуткові кутової швидкості 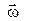 й радіуса обертання
й радіуса обертання 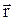 :
: 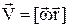 . Дійсно, величина швидкості
. Дійсно, величина швидкості 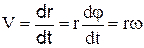 , а як вектор
, а як вектор 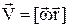 . Величина тангенціального прискоренняобертового руху дорівнює добуткові кутового прискорення b i радіуса кривизни r at=br. Дійсно, at=
. Величина тангенціального прискоренняобертового руху дорівнює добуткові кутового прискорення b i радіуса кривизни r at=br. Дійсно, at= 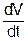 =
= 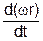 =r·
=r· 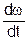 =br (r=const) , причому
=br (r=const) , причому 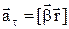 .
.
Час повного обороту (кут обертання 360 градусів) називається періодом T, а число повних оборотів за одиницю часу - частотою n=1/T, причому кут повороту за одиницю часу j = 2pn.
1.6.1. Похідна від одиничного вектора 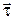
 Нехай орт
Нехай орт 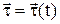 є функцією часу, тобто, залишаючись сталим за величиною (|
є функцією часу, тобто, залишаючись сталим за величиною (| 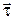 |=1), він може змінювати напрямок – обертатися з деякою кутовою швидкістю
|=1), він може змінювати напрямок – обертатися з деякою кутовою швидкістю 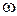 . При повороті на малий кут
. При повороті на малий кут 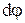 вектор
вектор 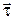 має приріст
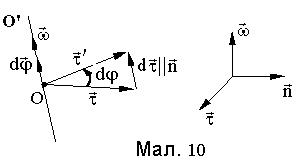
має приріст 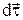 (див.Мал. 4). Цей приріст, як нескінченно малий, буде лежати на дотичній до кривої, що її описує кінець вектора
(див.Мал. 4). Цей приріст, як нескінченно малий, буде лежати на дотичній до кривої, що її описує кінець вектора 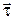 (годограф вектора), тобто він буде перпендикулярний вектору
(годограф вектора), тобто він буде перпендикулярний вектору 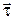 . Одиничний вектор, перпендикулярний вектору
. Одиничний вектор, перпендикулярний вектору 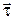 , є нормаллю
, є нормаллю 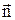 і
і 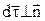 . За величиною
. За величиною 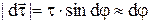 . Запишемо тепер похідну від
. Запишемо тепер похідну від 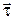
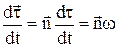 . (2)
. (2)
де величина 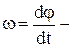 є миттєва швидкість обертання (обертова швидкість) вектора
є миттєва швидкість обертання (обертова швидкість) вектора 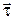 відносно миттєвої осі обертання ОО', яка перпендикулярна векторам
відносно миттєвої осі обертання ОО', яка перпендикулярна векторам 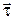 та
та 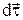 . Прийнято, що малому кутові повороту
. Прийнято, що малому кутові повороту 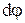 можна співставити вектор
можна співставити вектор 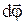 , який лежить на осі обертання і з його вершини видно, що обертання вектора
, який лежить на осі обертання і з його вершини видно, що обертання вектора 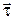 відбувається проти годинникової стрілки. У цьому випадкові кутовій швидкості співставляється вектор
відбувається проти годинникової стрілки. У цьому випадкові кутовій швидкості співставляється вектор 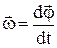 , який також лежить на осі обертання (див.Мал.10). Тепер вираз (2) можна записати у вигляді
, який також лежить на осі обертання (див.Мал.10). Тепер вираз (2) можна записати у вигляді
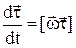 , (2')
, (2')
де векторний добуток 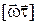 паралельний вектору
паралельний вектору 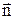 , а його величина
, а його величина 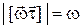 .
.
Дата добавления: 2015-09-18; просмотров: 1065;
