Прискорення, кривизна траєкторії

Прискорення криволінійного руху визначає зміну швидкості за напрямом та величиною. Прискорення(миттєве прискорення) - вектор, який є похідною від швидкості тіла по часу

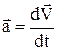. (1)

Кут між прискоренням матеріальної точки, що рухається по кривій, і її швидкістю може змінюватися від 0 до 180 градусів. Одиницею вимірювання прискорення є .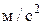

Середнєприскорення - вектор, який дорівнює відношенню приросту швидкості 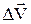до часу Dt, за який цей приріст стався

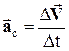. (2)

Важлиим є необхідність представити миттєве прискорення як суму двох складових, одна з яких визначає зміну швидкості за величиною, а друга визначає поворот вектора швидкості. Розглянемо це питання докладніше.

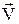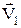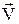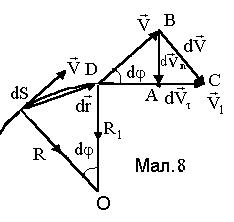
Нехай в час t тіло має швидкість , а в час t+dt - . Вектори та 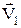є дотичними до траєкторії (див. Мал.8). Точка перетину нормалей до них визначає центр кола О, дуга якого dS співпадає з траєкторією dS. За радіус кола можна взяти R чи R₁, величини яких практично однакові і є радіусами кривизни траєкторії. Приріст вектора швидкості 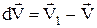, направлений відрізок 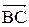шляхом проектування можна розкласти на два вектори: по нормалі - 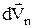, направлений відрізок 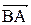та по дотичній до траєкторії - 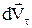, направлений відрізок 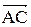. Ці складові називаються нормальною та тангенціальною складовими приросту швидкості відповідно. Вектор прискорення тепер можна записати у вигляді

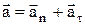, (3)

де 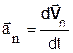- нормальне i 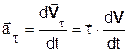- тангенціальне прискорення. Вектор 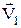за час dt повернуся відносно вектора 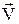на кут 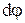. З малюнка видно, що dV_n=Vdj, а 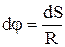і тому

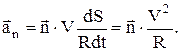(4)

З іншого боку

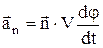. (5)

Кривизна траєкторіїза визначенням є

С= 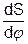, (6)

dj - кутова величина дуги dL. Для малих dj маємо dS=R·dj i кривизна траєкторіїможе бути записана у вигляді

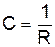. (7)

Таким чином кривизна траєкторії є величиною, оберненою до радіуса кривизни.

Розглянемо докладніше це питання з іншої точки зору. Знайдемо прискорення, підставивши в (1) значення вектора швидкості у вигляді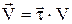

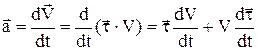. (8)

Підставивши в (8) вираз для похідної від тангенціального вектора 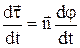одержимо

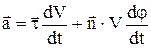. (9)

Таким чином ми одержали прискорення у вигляді суми тангенціального прискорення

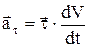(10)

та нормального прискорення

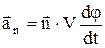, (11)

де j - кут повороту вектора швидкості. З (10-11) видно, що тангенціальна складова прискорення 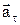визначає зміну вектора швидкості 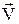за величиною, а нормальна складова 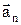- за напрямком.

Одиницею вимірювання прискорення є м/с².