Переріз поверхонь площинами. Розгортки

Площина перерізає поверхню в загальному випадку з деякої плоскої лінії. Для гранної поверхні – це багатокутник (рис.1.83), вершинами якого є точки перетину січної площини з ребрами, а сторонами – лінії перетину з гранями. Для кривої поверхні це можуть бути плоскі прямі або криві лінії – окружності, еліпси і т.ін., або їхні частини. Залежно від взаємного розташування поверхні й площини, перерізи можуть бути замкнутими й розімкнутими.

Проекціюванням на додаткову площину креслення завжди можна перетворити так, щоб січна площина стала проекціюючою, тому нижче, як правило, не розглядаються випадки перерізів поверхонь площинами загального положення.

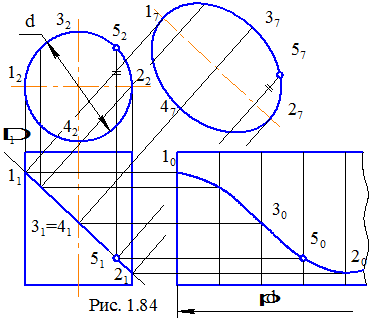На рис. 1.84 представлене креслення циліндричної поверхні обертання і січної горизонтально-проекціюючої площини Δ. Вісь поверхні є фронтально-проекціюючою лінією, і вся поверхня зображується на П₂ у вигляді окружності. Ця окружність є слідом-проекцією. Знаючи властивість проекціюючих елементів, виявляємо проекції перерізу: на головному зображенні воно збігається з окружністю, а на виді зверху – із слідом-проекцією січної площини.

Нагадаємо, що площина може перерізати розглянуту поверхню по прямим лініям (площина паралельна осі поверхні), по окружності (площина перпендикулярна осі поверхні) і по еліпсу (площина розташовується під довільним кутом до поверхні). Істинний вид перерізу – еліпс – одержимо на додатковій площині проекцій, що паралельна площіні Δ і перпендикулярна П₁.

Розгорткою називають плоску фігуру, одержувану при сполученні поверхні з площиною. Циліндрична поверхня обертання, обмежена двома окружностями, розгортається в прямокутник, одна сторона якого дорівнює його висоті (довжині твірної), а друга – довжині окружності. Лінія перерізу на розгортці представляє собою синусоїду.

Похила пірамідальна поверхня на рис. 1.85 обмежена горизонтальними відрізками АВ, ВР, АС, вершиною S і пересічена фронтальною площиною Г. Вид зверху плоского незамкнутого багатокутника перерізу зображується лінією, що збігається зі слідом-проекцією площини, і обмежений по довжині крайніми лініями горизонтальної проекції поверхні. Відзначивши на виді зверху точки перерізу ребер піраміди з площиною Г, будують фронтальні проекції, а, потім, з'єднавши їх прямими з урахуванням видимості, наносять зображення перерізу на площині проекцій П₂. Багатокутник перерізу зображується на цю площину неспотворено.

Розгортку пірамідальної поверхні виконують способом тріангуляції. Побудова зводиться до багаторазової побудови істинних величин трикутників, із яких складається поверхня, по їхніх сторонах. Тому, попередньо визначають істинну величину ребер піраміди, які займають загальне положення (AS і BS).

На рисунку показана побудова істинної величини одного ребра – BS, із указівкою положення точки 3, що належить перерізу. Положення ліній вигину на розгортці наносять тонкою штрих-пунктирною лінією з двома точками.

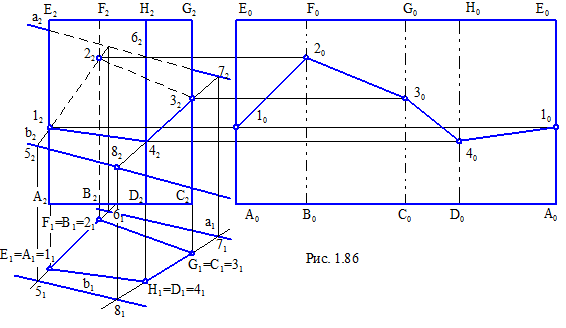На рис. 1.86 представлено креслення прямої чотирикутної призматичної поверхні, з горизонтально-проекціюючими гранями. Січна площина, що задана двома паралельними прямими Σ(а, b), є площина загального положення. Горизонтальна проекція 1₁2₁3₁4₁ багатокутника перетину збігається із зображенням призматичної поверхні на площині П₁.

Фронтальну проекцію перерізу визначають по її приналежності січній площині Σ(а, b). Для цього, горизонтальні проекції 1₁2₁ і 3₁4₁ ліній продовжують до перетину з визначником площини, потім отримані точки знаходять на фронтальній проекції, проводячи лінії 5₂6₂ і 7₂8₂ і на них, у межах проекцій граней, виділяють фронтальну проекцію чотирикутника перерізу.

Пряма призматична поверхня, обмежена відрізками прямих AB, BC і т.д., перпендикулярних її боковим ребрам, розгортається в прямокутник висотою, рівній висоті цієї поверхні й довжиною, рівній сумарній довжині обмежуючих відрізків. Нанесення на розгортку лінії перерізу зрозуміло з креслення.

Площина може перерізати конічну поверхню по окружності, еліпсу, параболі, гіперболі і по прямолінійним твірним. На рис. 1.87 наведена фронтальна проекція конічної поверхні обертання і показані сліди-проекції січних площин, які дають певний тип перерізу.

Площина Г, перпендикулярна осі поверхні, розсікає її по окружності; площина Δ, що перерізає так само всі утворюючі, але не перпендикулярна осі – по еліпсу; площина Σ, що паралельна однієї твірної лінії поверхні – по параболі; площина Ψ, що паралельна двом твірним, – по гіперболі (містить дві вітки: на нижній і верхній частинах поверхні); площина Ω, що проходить через вершину конічної поверхні, – по прямолінійних твірних лініях.

На рис. 1.88 зображена конічна поверхня обертання з вертикальною віссю, що пересічена горизонтально-проекціюючою площиною. Оскільки січна площина стосовно поверхні розташовується паралельно двом твірним (ці утворюючі показані на горизонтальній проекції конуса, вони паралельні сліду-проекції площини Δ₁), то в перерізі одержують гіперболу, горизонтальна проекція якої збігається зі слідом-проекцією площини.

Побудова фронтальної проекції гіперболи зручно почати з точок 1 і 2 на окружності, що обмежує конічну поверхню. Вершина гіперболи (точка 3) розташовується на твірній конуса S4, що на горизонтальній площині проекцій утворить прямий кут із слідом-проекцією площини Δ. Фронтальна проекція гіперболи розташована так, що частково лежить на видимій стороні конічної поверхні, частково – на невидимій. Границею видимості служить точка 5, що розташована на крайній правій твірній поверхні.

Для визначення проміжних точок гіперболи, на конічній поверхні проводять додаткові лінії, наприклад, окружність довільного радіуса. На горизонтальній проекції цієї окружності виділяють точки 6 і 7, що лежать на сліді-проекції січної площини Δ, і по лініях зв'язку визначають їхні фронтальні проекції. Положення точок 8 і 9 знаходять аналогічно.

Розгортка конічної поверхні обертання, обмежена окружністю, представляє сектор зі стороною, рівній довжині твірної конуса і з кутом при вершині α=R/L·360, де: R – радіус окружності, що обмежує поверхню; L – довжина твірної. Довжина дуги, що обмежує сек тор, дорівнює довжині окружності, що обмежує конічну поверхню.

Розглянемо ще одне завдання (рис. 1.89): через дві точки А і В, задані на окружності, що обмежує конічну поверхню, провести площину, що перерізає цю поверхню по параболі і побудувати проекції перерізу. Вісь поверхні займає фронтально-проекціююче положення.

Для рішення використаємо додаткову площину проекцій П₇, розташувавши її таким чином, щоб лінія, що з'єднує точки А і В, виявилася перпендикулярною до неї. У цьому випадку, січна площина, що проходить через точки, на площині проекцій П₇ зобразиться слідом-проекцією, який можна розташувати паралельно крайній твірній конічної поверхні. Вершину параболи знайдемо в точці перетину сліда-проекції січної площини з другою крайньою твірною S4 поверхні. Це буде точка 1. Для знаходження проекцій цієї точки на площинах проекцій П₂ і П₁, скористаємося проекціями твірної S4 (вони, звичайно, тут уже не будуть крайніми і їх необхідно побудувати). Проміжні точки на параболі можна побудувати аналогічно тому, як це робилося в попереднім завданні, тобто введенням додаткових ліній (окружностей) на поверхні.

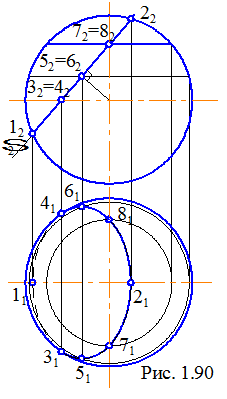
При перерізі сферичної поверхні площиною завжди утворюється окружність. Якщо січна площина паралельна площині проекцій, на цю площину окружність перерізу проектується без спотворення. Якщо січна площина займає проекціююче положення, (рис. 1.90), то одна проекція перерізу збігається зі слідом-проекцією, тобто зображується відрізком прямої, довжина якого дорівнює діаметру окружності перерізу, а на іншій площині проекцій – еліпсом, велика вісь якого (лінія 5₁6₁) займає проекціююче положення, і також дорівнює діаметру окружності переріза. Довжина малої осі залежить від кута нахилу січної площини. На горизонтальній площині проекцій еліпс будують по точках. Перетин частково розташований під екватором сфери, тому частина еліпса між точками 3₁1₁4₁ невидима.

◊ Як будується лінія перерізу поверхні площиною?

◊ Які лінії можуть бути отримані при перерізі циліндричної, конічної і сферичної поверхонь площинами?