Эффект Холла. Допустим, что у нас имеется прямоугольная металлическая пластинка, по которой течет постоянный ток с плотностью

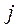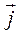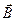Допустим, что у нас имеется прямоугольная металлическая пластинка, по которой течет постоянный ток с плотностью , направленный вдоль одного из ребер параллелепипеда. Поместив пластинку в однородное магнитное поле, направленное вдоль другого ребра. В 1879 году Холл обнаружил, что между гранями пластинки, параллельны векторам и возникает разность потенциалов

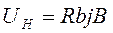(12)

Коэффициент пропорциональное в (12) называют постоянной Холла; b -толщина пластинки. Это явление получило название эффект Холла или галъвано-магнитного явления.

Наиболее просто ЭХ объясняется классической электронной теорией. На электроны, движущиеся в пластинке воздействует магнитная составляющая силы Лоренца, в результате чего у них появляется составляющая скорости направленная к верхней грани пластинки. У этой грани образуется избыток от­рицательных носителей тока, а у противоположной - избыток положительных. Возникает электрическое поле с напряженностью 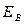, действие которого ком­пенсирует действие силы Лоренца. В стационарном состоянии

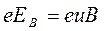или (13)

Умножим (13) на b и выразим и через плотность тока: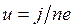

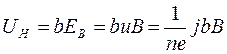(14)

Тогда в левой части получаем разность потенциалов и, сравнивая с (12), най­дем: значение постоянной Холла:

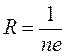(15)

Таким образом, измерив постоянную Холла, можно рассчитать концентрации но­сителей тока в проводнике.

Одним из важных параметров проводящих материалов является подвижность носителей тока. По определению подвижностью называется величина, равная средней скорости направленного движения носителей тока в электричес­ком поле единичной напряженности:

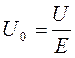(16)

Если соотношение 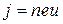разделить на Е , то, учитывая закон Ома и (16), получим важное соотношение:

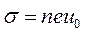(17)

Очевидно, что, измерив постоянную Холла и проводимость материала, можно рас­считать подвижность (холловскую) и концентрацию носителей тока.