Закон Ома для неоднородного участка цепи
ЗО в дифференциальной форме имеет вид: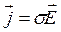
с другой стороны плотность тока определяется скоростью направленного движения носителей тока, и, если они имеют одинаковые знаки, 
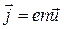. Сравнивая эти две формулы, можно заключить, что скорость упорядоченного движения 
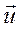носителей тока пропорциональна напряженности электрического поля. Отметим, что такая связь может наблюдаться только в том случае, если кроме силы вызывающей движение, на тело действует сила сопротивления среды. Эта сила обусловлена взаимодействием носителей тока с веществом проводника и приводит к существованию сопротивления проводников.
Очевидно, что если на участке цепи, кроме электростатической силы, действуют сторонние силы, то средняя скорость упорядоченного движения будет пропорциональна результирующей силе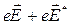
, а значит
|
|
|
|
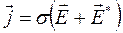
Формула (17.18) выражает закон Ома для неоднородного участка цепи в дифференциальной форме.
Получим выражение для ЗО в интегральной форме для неоднородного участка цепи. Рассмотрим внутри неоднородного участка цепи линию, такую, что в любом сечении, перпендикулярном к ней величины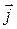 
, 
, 
, 
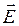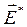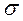имеют одинаковые значения, а направлены 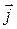, , 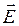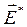по касательной к линии. Такую линию называют контуром тока. Выберем направление движения по контуру например от 1 к 2. Спроектируем (17.18) на некоторый элементов 
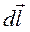контура:
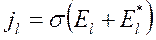
Проекции векторов будут равны их модулям, взятым со знаком, зависящим от направления соответствующего вектора. Сила тока в каждом сечений контура должна быть одинаковой, т. к. в противном случае в сечении будет накапливаться заряд. Выразив плотность тока через его силу, получим из (17.19):
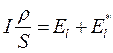
Умножим (17.20) на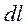 
и проинтегрируем вдоль участка контура:
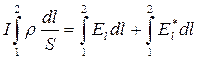
После интегрирования получаем:
|
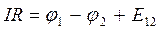
В (17.22) сила тока и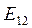 
являются алгебраическими величинами: если ток направлен вдоль направлений движений по контуру, то он положителен; ЭДС положительна в том случае, если она способствует движению носителей тока в выбранном направлении.
Разделив (17.22) на R, получим выражение для ЗО в интегральной форме для неоднородного участка цепи:
|
Соответственно для замкнутой цепи
|
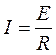
Дата добавления: 2015-09-14; просмотров: 728;