ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА.

Экспериментально установлено, что ВЭ идеального газа зависит только от температуры идеального газа, причем пропорциональна ей:

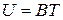(7.5)

Это отражает тот факт, что молекулы идеального газа не взаимодействуют друг с другом на расстоянии. В противном случае ВЭ идеального газа должна была бы зависеть от среднего расстояния между молекулами, т.е. от величины, пропорциональной .

Теплоемкость тела будем называть величину, равную отношению количества тепла 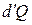, сообщенного телу, к изменению температуры тела 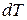, обусловленному этим процессом:

(7.6)

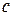Теплоемкость моля вещества называется молярной - , единицы массы – - удельной. Очевидно, что

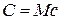(7.7)

Величина теплоемкости зависит от условий, в которых происходит нагревание. Поэтому, различают теплоемкость при постоянном объеме 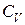и при постоянном давлении .

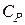При постоянном объеме - 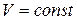- макроскопическая работа не совершается 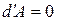, и из первого начала термодинамики следует:

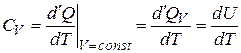(7.8)

Для моля идеального газа, дифференцируя соотношение (7.6), находим:

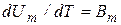(7.9)

Сравнивая соотношения (7.8) и (7.9), приходим к выводу о том, что коэффициент пропорциональности в (7.5) для внутренней энергии одного моля совпадает с удельной теплоемкостью при постоянном объеме, т.е.

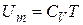(7.10)

Внутренняя энергия произвольной массы 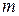газа, содержащей 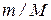молей,

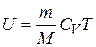(7.11)

При постоянном давлении нагревание сопровождается увеличением объема и совершением газом работы над внешними телами. Поэтому для нагревания на 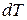потребуется

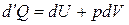. (7.12)

Соответственно для одного моля, разделив (7.12) на 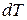, найдем:

(7.13)

Из уравнения состояния следует, что

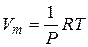. (7.14)

и при постоянном давлении

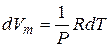. (7.15)

Подставив (7.15) в (7.13), получаем

. (7.16)

Соотношение (7.16) называется уравнением Майера. Из него вытекает физический смысл газовой постоянной R: она равна работе, совершаемой одним молем идеального газа при повышении его температуры при постоянном давлении на 1К. Отметим, что .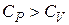

Отношение теплоемкости при постоянном объеме к теплоемкости при постоянном давлении 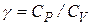является характерной константой для каждого газа, смысл которой мы выясним в дальнейшем. Воспользовавшись уравнением, Майера, найдем, что

. (7.17)

Выразив 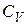из соотношения (7.17), найдем:

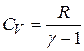. (7.18)

Тогда для энергии идеального газа справедливы соотношения:

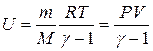. (7.19)