Внутренняя энергия идеального газа
Важной величиной в термодинамике является внутренняя энергия тела. Любое тело кроме механической энергии может обладать запасом внутренней энергии, которая связана с механическим движением атомов или молекул, составляющих тело, а также с их взаимодействием. Для идеального газа его внутренняя энергия является энергией молекулярно-кинетического движения атомов или молекул этого газа. Средняя кинетическая энергия поступательного движения молекулы согласно равенству (10.10) зависит только от температуры и равна E = 3kT/2 . Скорость молекул связана со своими составляющими по осям x , y и z соотношением 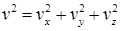 . Умножая это равенство на m/2 , получим
. Умножая это равенство на m/2 , получим 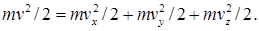 . Из последнего равенства следует, что кинетическая энергия поступательного движения молекул складывается из трех независимых составляющих, связанных с осями координат. Поэтому говорят, что молекула имеет три степени свободы движения.
. Из последнего равенства следует, что кинетическая энергия поступательного движения молекул складывается из трех независимых составляющих, связанных с осями координат. Поэтому говорят, что молекула имеет три степени свободы движения.
Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано положение системы. Для одноатомного газа, например гелия, каждый атом однозначно определяется заданием трех координат. Поэтому для одноатомного газа число степеней свободы i = 3 . Энергией вращательного движения одноатомная молекула практически не обладает, так как ее масса сосредоточена в ядре. В силу хаотичности движения атомов средние значения энергии, приходящиеся на каждую степень свободы движения, будут одинаковыми и равными третьей части от энергии поступательного движения, т.е. равными kT/2 . Полная средняя энергия поступательного движения молекулы может быть представлена в виде eпост = i kT/2 .
Если молекула газа состоит из трех или более атомов, то при хаотических соударениях молекул энергия поступательного движения молекул будет переходить в энергию вращательного движения молекул и наоборот. В результате этого получается, что средние энергии поступательного и вращательного движения многоатомных молекул одинаковы. Вращение многоатомной молекулы может происходить относительно трех независимых осей и его можно описать с помощью трех угловых величин. Поэтому вращательное движение имеет также три степени свободы движения. Полное число степеней свободы движения молекул многоатомного газа i = iпост + iвр = 3 + 3 = 6 . Причем полную кинетическую энергию многоатомной молекулы можно записать в виде
e = i kT/2. (10.1)
Полученный результат Максвелл обобщил в принципе равного распределения энергии: в системе, состоящей из большого числа частиц, механическая энергия распределяется поровну между их степенями свободы движения.
 Эксперимент подтверждает этот принцип. Например, двухатомная молекула в среднем обладает энергией вращательного движения относительно лишь двух осей вращения y и z (рис.10.1), и поэтому обладает двумя степенями свободы вращательного движения. Общее число степеней свободы движения двухатомной молекулы i = iпост+ iвр= 3 + 2 = 5.
Эксперимент подтверждает этот принцип. Например, двухатомная молекула в среднем обладает энергией вращательного движения относительно лишь двух осей вращения y и z (рис.10.1), и поэтому обладает двумя степенями свободы вращательного движения. Общее число степеней свободы движения двухатомной молекулы i = iпост+ iвр= 3 + 2 = 5.
Для киломоля идеального газа, содержащего NA число молекул, внутренняя энергия в соответствии с выражением (10.1) определяется соотношением Um = NA i kT/2 или
Um = i RT/2, (10.2)
где R - универсальная газовая постоянная. Выражение (10.2) показывает, что внутренняя энергия киломоля является функцией лишь от температуры газа. Для произвольной массы газа m получим U = i(m/m)RT/2 , где m - моль газа.
В реальном газе между молекулами действуют силы притяжения, которые при расширении газа будут совершать работу. Поэтому его внутренняя энергия будет зависеть не только от температуры, но и от объема. Для реального газа внутренняя энергия будет являться функцией только от температуры и объема: U = f(T,V) . Если реальный газ вернется в некоторое прежнее состояние, то его внутренняя энергия будет иметь прежнее значение.
Дата добавления: 2015-11-04; просмотров: 1278;
