ПРЕОБРАЗОВАНИЕ И СЛОЖЕНИЕ СКОРОСТЕЙ

Рассмотрим движение некоторой частицы. Её скорость в системе отсчета 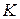определяется выражениями:

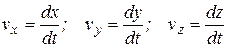. (6.16)

Аналогичные выражения справедливы, естественно, и в системе .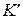

Из преобразований Лоренца вытекают соотношения:

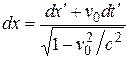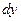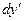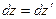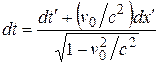; = ; ; (6.17)

Тогда для составляющих скорости в 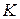имеем:

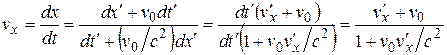. (6.18)

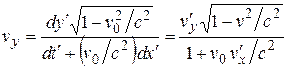. (6.19)

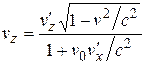. (6.20)

В соотношениях (6.18) - (6.20) составляющая скорости вдоль оси 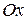на первый взгляд имеет привилегированное положение. Однако это в действительности есть только следствие специального выбора ориентации осей рассматриваемых систем отсчета.

Если тело движется вдоль оси 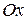, то его скорость совпадает с проекцией на эту ось, и закон сложения скоростей имеет вид:

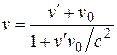. (6.21)

Допустим что в системе 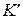движется частица с 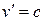. Тогда в системе отсчета 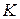, неподвижной, ее скорость будет равна:

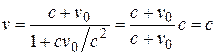. (6.22)

в соответствии с постулатом о постоянстве с.