ИНТРЕВАЛ.

Итак, как мы установили, пространство, и время в теории относительности не являются абсолютными и безотносительными к чему-либо, как это предполагалось в ньютоновской механике. Наоборот, пространство и время оказываются взаимосвязанными образуя единое пространство-время.

В связи с этим в теории относительности рассматривают воображаемое четырехмерное пространство, по трем осям которого откладываются пространственные координаты, а по четвертой пропорциональная времени временная координата 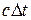, имеющая ту же размеренность, что и пространственные координаты. В этом пространстве всякое событие, характеризуемое временем, когда оно произошло, и местом, где оно произошло, изображается точкой с координатами 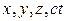. Эту точку называют мировой точкой.

Всякой частице соответствует линия, называемая мировой линией, которая для покоящейся частицы будет параллельна оси .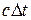

В обычном трехмерном пространстве величина расстояния между двумя точками

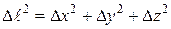(6.9)

является инвариантом, т.е. не изменяется при переходе от одной инерциальной системы координат к другой.

В четырехмерном пространстве величина

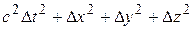(6.10)

не является инвариантом. Следовательно, эта величина не обладает свойствами расстояния между двумя мировыми точками.

В четырехмерном пространстве инвариантом является другая величина, а именно

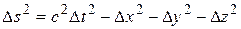(6.11)

Эту величину по определению называют интервалом между событиями. Учитывая (6.9), для интервала можно записать:

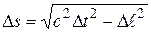(6.12)

Покажем, что интервал действительно является инвариантом по отношению к преобразованиям Лоренца. В соответствии с формулами преобразований Лоренца (6.3)

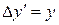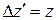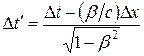; ; ; (6.13)

Подставив (6.13) в определяющее интервал соотношение (6.10), получим:

			Уничт.

.

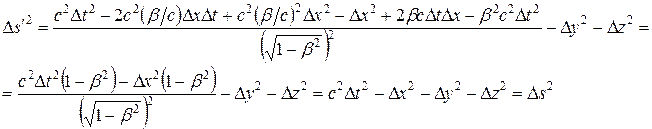Таким образом, интервал действительно является инвариантом, хотя величины, из которых он составлен, как мы установили, таковыми не являются.

Выражение (6.8) для промежутка собственного времени можно преобразовать следующим образом:

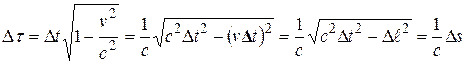(6.14)

Таким образом, промежуток собственного времени пропорционален интервалу между двумя рассматриваемыми событиями, и (как и интервал!) является инвариантом.

В соответствии с определением , в зависимости от соотношения между расстоянием 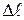, разделяющим точки в которых произошли два события и расстоянием 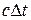, которое может пройти световой сигнал за время между событиями, интервал может быть вещественным, мнимым или равным нулю.

Если интервал равен нулю, то он разделяет события типа испускания светового сигнала в одной точке и его прием в другой. Только в этом случае Δ = .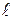

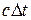Вещественный интервал, в силу его инвариантности, будет вещественным в любой системе отсчета, а значит в любой системе отсчета

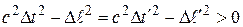(6.15)

События, разделенные вещественными интервалами, ни в какой системе отсчета не могут быть одновременными. Действительно, если бы такая система нашлась, то в ней разность 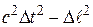должна была бы отрицательной, а интервал - мнимым. А этого не может быть в силу инвариантности интервала.

В то же время можно доказать, что для событий, разделенных вещественными интервалами существует система отсчета, в которой они будут пространственно совмещены. Такие свойства вещественных интервалов позволили назвать их времениподобными. События происходящие с одной частицей обязательно разделены времениподобными интервалами, т.к. частица не может двигаться со скоростью 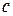, а значит путь, пройденный ею за 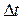будет меньше, чем 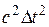. Можно доказать, что события, происходящие с одной частицей во всех системах отсчета происходят в одной последовательности.

Мнимые интервалы обладают обратными свойствами: события разделенные ими ни в одной системе отсчета не могут быть пространственно совмещены. Поэтому мнимые интервалы называют пространственноподобными. В то же время всегда можно найти такую систему отсчета, в которой события, разделенные мнимыми интервалами будут происходить одновременно.

Расстояние Δℓ между точками, в которых произошли события, разделенные пространственноподобными интервалами, обязательно больше, чем 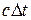. Поэтому такие события не могут оказать влияния друг на друга и не могут быть причинно связанными.